OTA/VCA/PGA を使用した 2 次特性 VCF (2) - シンセ・アンプラグド

下の図の OTA による回路での LPF 入力から LPF 出力までの伝達関数を求めてみます。
まず、A1、C1、B1 および β の「ローカル・フィードバック」を行っている「不完全積分器」の部分の伝達関数 G(s) を求めます。

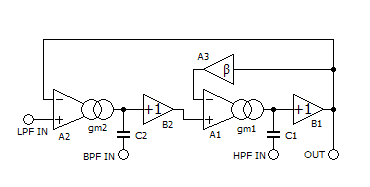
A1、C1 および B1 だけから成る (完全) 積分器の伝達関数は (gm₁/C₁)(1/s) で、負帰還ループにのみ「β」が掛かっていますから、フィードバック込みの「不完全積分器」としての伝達関数 G(s) は、
$\qquad\qquad G(s) \,=\, \large\frac{\frac{{gm}_1}{C_1}\cdot \frac{1}{s}}{ 1 \,+\, \beta \cdot \frac{{gm}_1}{C_1}\cdot\frac{1}{s}} \,=\, \frac{\normalsize\frac{\normalsize 1}{\normalsize \tau_1^{\,}}}{\normalsize s \,+\, \beta^{\,} \cdot \frac{\normalsize 1}{\normalsize \tau_1^{\,}}} \,=\, \frac{\normalsize \omega_1}{\normalsize s \,+\, \beta^{\,} \cdot \omega_1}$
となります。
ここで、時定数 τ₁ および角周波数 ω₁ は

$\qquad \qquad \tau_1 = 1 / \omega_1 = C_1 / gm_1$

で定義されます。
この G(s) を見ると、1 次 LPF の伝達関数になっていることが分かります。
A2 側の完全積分器を含む、LPF IN から出力までの全体の伝達関数 F(s) は、
$\qquad\qquad F(s) \,=\, \large\frac{\frac{{gm}_2}{C_2}\cdot \frac{1}{s} \cdot G(s)}{1 + \frac{{ gm}_2}{C_2}\cdot \frac{1}{s} \cdot G(s)} \,=\, \frac{\normalsize \omega_1 \,\cdot \,\omega_2}{\normalsize s^2 \,+\, \beta^{\,} \cdot \omega_1 \cdot s \,+\, \omega_1 \,\cdot \,\omega_2}$
と表されます。
ここで、時定数 τ₂ および角周波数 ω₂ は

$\qquad \qquad \tau_2 = 1 / \omega_2 = C_2 / gm_2$

で定義されます。
この F(s) を、一般の (全極型) 2 次 LPF の伝達関数
$\qquad\qquad T(s)\,=\, \frac{\normalsize H \cdot (\omega_0)^2}{\normalsize s^2 \,+\, \frac{\normalsize \,\omega_0^{\,}\,}{\normalsize Q} \cdot s \,+\, (\omega_0)^2}$
と比較します。
ここで、ω₀ は LPF のカットオフ角周波数、Q はピークの鋭さを表す数、H は LPF の DC でのゲインです。
まず、H = 1 が強制されるので、この構成では LPF の DC ゲインが持てないことが分かります。
ただし、実際の LM13700 などの回路では、差動入力の抵抗分圧回路の分圧比を調整することにより、ゲインの設定は可能です。
ほかには、
$\qquad\qquad (\omega_0)^2 = \omega_1 \cdot\, \omega_2$
$\qquad\qquad \omega_0 \,=\, \sqrt{\omega_1^{\,} \cdot\, \omega_2} \,=\, \frac{1}{\sqrt{\tau_1^{\,} \cdot\, \tau_2}}\,=\, \frac{\sqrt{gm_1^{\,} \cdot\, gm_2}}{\sqrt{C_1^{\,} \cdot\, C_2}}$
$\qquad\qquad Q = \frac{1}{\,\beta\,} \cdot \,\frac{\omega_0}{\,\omega_1_^{\,}} \,=\, \frac{1}{\,\beta\,}\cdot\,{\sqrt{\frac{\,\tau_1^{\,}\,}{\tau_2^{\,}\,}}\,=\, \frac{1}{\,\beta\,}\cdot\,{\sqrt{\frac{\,\omega_2^{\,}\,}{\omega_1^{\,}\,}}\,=\, \frac{1}{\,\beta\,}\cdot\,{\sqrt{\frac{\,C_1^{\,}\,}{C_2^{\,}\,}}\cdot\,{\sqrt{\frac{\,{gm}_2^{\,}\,}{{gm}_1^{\,}\,}}$
という関係が導かれます。
カットオフ周波数 ω₀ は gm₁ と gm₂ の積の平方根に比例し、C₁ と C₂ の積の平方根に反比例します。
通常 C₁、C₂ の値は設計時に決定するものであり、動作時に動的に変更することはなく、gm の方を電圧制御します。
オーソドックスな方法では、gm₁ と gm₂ とを同じ値 gm₀ に選び、同じように変化させます。
この場合、
$\qquad\qquad \omega_0 \,=\, \frac{1}{\sqrt{C_1^{\,} \cdot\, C_2}}\,\cdot\, gm_0$
となり、カットオフ角周波数 ω₀ と gm₀ とが比例することになります。
Q については、(1/β)、sqrt(C₁/C₂)、sqrt(gm₂/gm₁) の 3 つの因子の積になることが分かります。
これら 3 つの値のいずれか、あるいは複数を電圧制御すれば、フィルタの Q、つまりレゾナンスの電圧制御が実現できます。
オーソドックスな方法では、β の値を OTA や VCA で電圧制御します。
gm₁ と gm₂ とを同じ値 gm₀ に選ぶ場合、sqrt(gm₂/gm₁) = 1 となり、この因子は変化しません。
β = 1 と選ぶ場合、あるいは β を一定値のまま変化させない場合には、電圧制御可能なのは gm の因子のみとなります。
ここで β = 1 と選び、
$\qquad\qquad \omega_1 \,=\, \omega_0 \,/\, Q$
$\qquad\qquad \omega_2 \,=\, \omega_0 \,\cdot\, Q$
と置き、計算すると、
$\qquad\qquad \omega_1 \,\cdot\, \omega_2 \,=\, (\omega_0 \,/\, Q)\cdot(\omega_0 \,\cdot\,Q) \,=\, (\omega_0)^2$
$\qquad\qquad \frac{1}{\,\beta\,}\,\cdot\,\sqrt{\frac{\,\omega_2^{\,}}{\omega_1}} \,=\, \sqrt{\frac{\omega_0 \,\cdot\,Q}{\omega_0 \,/\, Q}}\,=\, Q$
となり、これは上で求めた ω₀ と Q の式に一致します。
つまり、ω₁、ω₂ を常に同じ値 ω₀ にするのではなく、1/Q 倍および Q 倍した値に選ぶと、電圧可変要素 2 個でカットオフ周波数とレゾナンスとを電圧制御できることが分かります。
ただし、gm₁ と gm₂ との値の「拡がり」は大きくなり、Q = 10 でも gm₁ と gm₂ との比は Q² = 100 倍にもなります。
dB で表現すると 40 dB であり、カットオフ周波数 20 〜 20 kHz の 60 dB の gm 可変レンジに 40 dB が加わって、合計で 100 dB のレンジが必要になります。
OTA の gm を決めるバイアス電流には制限があり、LM13700 の場合絶対最大定格で 2 mA、推奨動作の上限が 0.5 mA ですから、レンジを拡大するのは電流の小さい方に伸ばすしかありません。
また、gm の設定値に Q を掛けたり、Q で割ったりするのは複雑になるような気がしますが、実際には gm を決めるバイアス電流はアンチログ回路で生成されているので、その特性を利用すれば比較的簡単に実現できます。
アンチログ回路で、入力電圧を「真数」と見れば出力電流は「指数」であり、出力電流を「真数」と見れば入力電圧は「対数」となります。
したがって、gm を決めるバイアス電流での「掛け算」、「割り算」は、「対数」のドメインのアンチログ入力電圧では「足し算」、「引き算」になります。
例を示すと、トランジスタのコレクタ電流が 10 倍になる差動ベース電圧は約 60 mV なので、アンチログ電流出力トランジスタは gm₁ 用と gm₂ 用の 2 組設けたうえで、gm₂ 側のベース電圧に約 60 mV を加え、gm₁ 側のベース電圧を約 60 mV 減らすと、それぞれ 10 倍、1/10 倍が実現できます。
もちろん、そのために必要となる追加分の回路の量が、普通にレゾナンス用の電圧制御要素を設ける場合を上回ってしまうと意味がありません。
電子ボリウムなどの、ディジタル値でゲインを設定する PGA(Programmable Gain Amplifier) を使用する場合、カットオフ周波数のコントロールのために 2 組使うのが普通なので、ゲインはそれぞれ独立に設定可能です。
たとえば、NJW1159 (JRC) では、16 ビット相当の 95 dB レンジなので、例に示した Q = 10 程度は実現できます。
ただし、ゲインは 1 dB ステップでの設定であり、これは約 2 半音 (全音) ステップに相当するので、NJW1159 単独ではカットオフ周波数のコントロールだけでも解像度が足りません。
1 dB 以下のステップでゲイン設定可能な回路を追加する必要があります。
次回は LTSpice シミュレーションを行います。