OTA/VCA/PGA を使用した 2 次特性 VCF (3) - シンセ・アンプラグド

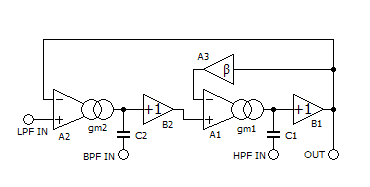
この回路を LTSpice で AC 解析するための回路図を下に示します。
各素子の値は直接には指定せず、「パラメタ」として表現しています。
OTA (gm セル) として、SPICE 組み込みの「G エレメント」(電圧制御電流源) を使用しています。

LPF / BPF / HPF の各入力には、それぞれ独立電圧源 (V エレメント) を接続し、入力としない電圧源は AC 0V と指定し、入力として使用する電圧源には AC 1V を指定します。
回路的には、ローカル・フィードバック・ループ内に β 倍の要素を含み、上の設定では、β を変化させて Q を可変しています。
カットオフ周波数の可変については自明なので、カットオフ周波数は 1 kHz に固定し、Q を、0.5、1、2、4、8 と .step ディレクティブ (ドット・コマンド) で変化させています。
結果のプロットを下に示します。

β = 1 と固定し、gm₁ と gm₂ との比を変化させて Q を可変する方式では、回路のトポロジーは上の場合と全く同じで、下に示すパラメタの設定だけを変更します。

結果は全く同じになるので、グラフは省略します。
また、BPF および HPF 動作の場合のグラフについても省略します。
この「最も簡単な」回路で、gm の比で Q を設定する方式では、大きな Q の場合にダイナミック・レンジの問題が生じます。
LPF 入力に対しては、

「初段」となる A2 側の OTA の gm₂ は Q 倍されているので大きく、
「2 段目」の A1 側の OTA の gm₁ は 1/Q 倍されているので小さく

なり、LPF の入力信号は A2 で大きく「増幅」されたあと、A1 で「減衰」されます。
したがって、たとえ LPF 出力端でそこそこの大きさとなるはずの信号でも、初段の出力端では大きなレベルとなり、クリッピングが生じる可能性が大きくなります。
通常の biquad 回路での縦続順序、つまり、
不完全積分器 (1 次 LPF) --- 完全積分器
という順序の構成では、このような問題は生じません。
ただし、「減衰」させた信号を「増幅」する形になるので、ノイズの点では不利です。
今回のシミュレーションでは、gm の値に対する乗算、除算を「回路的」にではなく、パラメタの「数値演算」で実現しましたが、次回のシミュレーションでは、OTA に LM13700 のマクロモデルを使い、gm の乗算、除算については、もう少し回路的なアプローチで実現します。