Gilbert Sine Shaper (14)

GSS

MOS FET の差動ペアの式のフーリエ変換の公式を見つけられないと書きましたが、それに近い公式を見つけました。
「岩波　数学公式」第 II 巻、§53、pp.276 に次のような式が載っていました。

\qquad\qquad f(x) = \begin{cases} \qquad \frac{\large x}{\large (a^2-x^2)^{\nu+(1/2)}} \qquad\qquad &[\; |x| \,\lt a\; ] \\ \vspace{10pt} \\ \qquad 0 & [\; |x|\, > a\;] \end{cases}
\hspace{100pt} [\; \mathfrak{R}\nu \,<\, 1/2 \; ]
\qquad
\qquad\qquad F(y) = \frac{\large i\, a\, \mathrm{sgn}\, y}{\sqrt{\large 2}} \Gamma\left(\,\frac{\,1\,}{2}-\nu \,\right)\, \left| \frac{y}{\,2 a\,}\right|^\nu J_{\fs1 1-\nu}(a | y |)

ここで、a は正の数、\nu は実部が 1/2 以下の複素数、\Gamma(\cdot) はガンマ関数、J_n(\cdot) は n 次の第一種ベッセル関数です。
\mathrm{sgn}\,y は y の値に応じて、
\qquad\qquad \mathrm{sgn}\,y = \begin{cases} \quad +1 \qquad\qquad &[ \; y \,\gt\, 0\; ] \\ \quad 0 & [\; y= 0 \;] \\ \quad -1 & [\; y \,\lt\, 0\;] \end{cases}
となる関数です。
MOS FET の差動ペアの「S 字カーブ」の関数 g(x) を
\qquad \qquad g(x) = x \sqrt{1 - x^2/4} = \left(\frac{\large\,x\,}{2}\right)\sqrt{2^2 - x^2}
と変形すると、a = 2,\; \nu = -1 と選んでやれば、全体の係数 1/2 を除いては、上に示した公式の f(x) の場合分けの上側に一致することが分かります。
違うのは、MOS FET の場合は場合分けの条件が |x|\,\lt\,\sqrt{2} となり、それ以外の領域では関数値が +1 あるいは -1 の値になることです。
変形した g(x) を ±2 までの範囲でグラフに描くと、

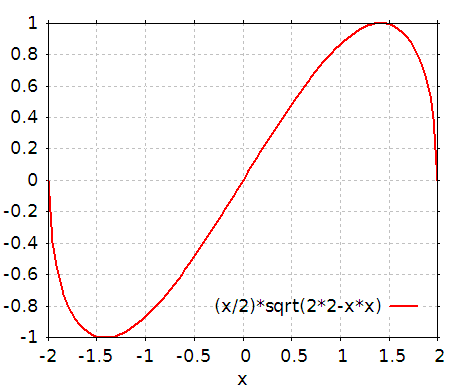
となります。　この図の範囲外では g(x) = 0 となります。
MOS FET の場合は \pm \sqrt{2} から外の領域での形が違うので、残念ながら上の公式は適用できません。
そこで、上の公式の f(x) そのものをプログラムで扱うようにして、FFT 結果と理論式を比べてみることにしました。
まず、g(x) の級数を計算して、FFT を掛ける前の「時間波形」に相当するものを示します。

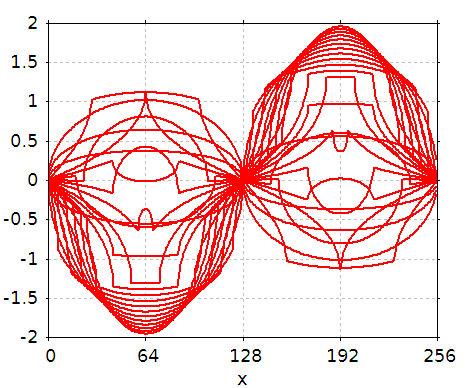
これをみると、非常に奇妙な波形になっています。　E/Vt が大きい時は振幅も大きく、波形も途中が折れ曲がった正弦波という感じですが、E/Vt が小さくなると波形には大きな変化が現れます。
一方、理論式のほうは、上の公式を利用して(逆)フーリエ変換を求めると、y\,\gt\,0 として、
\qquad \qquad \begin{eqnarray} G(y) & = & \frac{\large -i \cdot 2}{\large 2 \sqrt{2}}\left( \frac{\,\sqrt{\large \pi}\,}{\large 2}\right)\left(\frac{\large\,2\cdot 2\,}{\large y}\right) J_{\fs1 1-(-1)}(2 \cdot y) \\ \vspace{10pt} \\ &=& -i \,\frac{\sqrt{\large\, 2 \pi\,}}{\large y} J_{\fs1 2}(2 \cdot y)\end{eqnarray}
となります。
高調波の振幅を表す \eta の式は、\beta = E/(2V_t) として、
\qquad\qquad \begin{eqnarray} \eta(n) &=& i \cdot \frac{\large\, 2 \sqrt{2 \pi}\,}{\beta} G\left( \frac{\large\, n \cdot \pi\,}{\beta} \right)\\ \vspace{10pt} \\ &=& \frac{\large\,2\cdot 2 \pi \,}{\beta}\left(\frac{\beta}{\large \,n\cdot\pi\,}\right)J_2\left(\frac{2 n \pi}{\beta}\right) \\ \vspace{10pt} \\ &=& \frac{\,\large 4\,}{\large n} J_2\left( 4 n \pi \cdot V_t / E\right)\end{eqnarray}
という、見た目はシンプルな式となりました。 (11/11 追記：誤りを訂正しました)
この理論式の結果を赤い線で、FFT 結果を青い線でプロットしたグラフを下に示します。

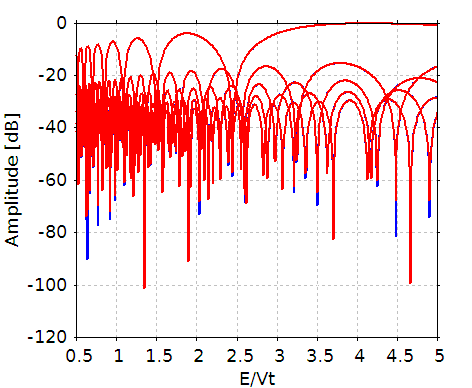
両者は、ほとんど重なっており、数値的には有効数字 3 桁程度で一致しています。
前の tanh 関数の場合には有効数字 6 桁まで一致していましたから、それに比べると精度が低いです。
「時間波形」は非常に奇妙な形なのに、その高調波成分の振幅の値はとてもシンプルな形で与えられるのが興味深いです。　とは言っても、ベッセル関数なので、中身は単純ではありません。