dsPIC33FJ64GP802 (24) --- 周波数シフター (8)

　偶対称の位置に配置した方形波のフーリエ展開である 1.442-4. 式のサイン → コサイン置き換え版である 1.442-3. 式

$\hspace{-5em} \displaystyle \sum_{k\;=\;1}^\infty (-1)^{k-1}\frac{\sin (2k-1) x}{2k-1} = \frac{1}{2}\ln\tan\left(\frac{\pi}{4}+\frac{x}{2}\right) \qquad [-\pi < x < \pi ] \tag{1.442-3.}$

と、前回示した逆グーデルマン関数の定義

$\hspace{0em}\displaystyle \begin{align} x = \mathrm{gd}^{-1}\ u = \int_{0}^{u} \frac{dt}{\cos t} = \ln \tan \left( \frac{u}{2} + \frac{\pi}{4} \right) \end{align}$

の右辺を比較すると、

係数 $\frac{1}{2}$ の有無

変数 $x$ と変数 $u$ の違い

を除いては同じ形になっていることが分かります。
　変数の違いは、単に逆グーデルマン関数の定義で、たとえば、 $x \rightarrow y$ および $u \rightarrow x$ と置き換えてやれば一致させることができます。
　そうすると、

$\hspace{0em}\displaystyle \begin{align} \frac{y}{2} = \frac{1}{2}\mathrm{gd}^{-1}\ x = \frac{1}{2}\ln \tan \left( \frac{x}{2} + \frac{\pi}{4} \right) = \sum_{k\;=\;1}^\infty (-1)^{k-1}\frac{\sin (2k-1) x}{2k-1} \end{align}$

となり、1.442-3. 式を逆グーデルマン関数で表すことができます。
　最後に、三角波の場合を示します。

$\hspace{-5em} \displaystyle \sum_{k\;=\;0}^\infty (-1)^{k}\frac{\sin (2k +1) x}{(2k+1)^2} = \begin{cases}\displaystyle \frac{\pi}{4} x & [-\frac{\pi}{2} < x < \frac{\pi}{2} ] \\ \mathstrut \\ \displaystyle \frac{\pi}{4} \left( \pi - x \right) & [\frac{\pi}{2} < x < \frac{3\pi}{2} ] \end{cases} \tag{1.444-5.}$
$\hspace{-1em}\displaystyle \begin{align} \sum_{k\;=\;1}^\infty \frac{\cos(2k-1)x}{(2k - 1)^2} &= \frac{\pi}{4}\,\left( \frac{\pi}{2} - |x| \right) & [-\pi < x < \pi ] \tag{1.444-6.} \end{align}$

　1.444-5. 式では $(2 k + 1)$ を使って表されており、一方、1.444-6. 式では $(2 k - 1)$ を使って表されていて、統一されていませんが、おそらく、これは別々の文献が「元ネタ」となっており、それぞれの表記の違いを受けついているものと思われます。
　実際に計算される値としては、1.444-5. 式では初項が $k = 0$ なので、

$\hspace{0em}\displaystyle \begin{align} (2 k + 1 ) & = (2 \cdot 0 + 1) = 1 \\ (2 k + 1 ) & = (2 \cdot 1 + 1) = 3 \\ (2 k + 1 ) & = (2 \cdot 2 + 1) = 5 \\ & \vdots \end{align}$

　一方、1.444-6. 式では初項が $k = 1$ なので、

$\hspace{0em}\displaystyle \begin{align} (2 k - 1 ) & = (2 \cdot 1 - 1) = 1 \\ (2 k - 1 ) & = (2 \cdot 2 - 1) = 3 \\ (2 k - 1 ) & = (2 \cdot 3 - 1) = 5 \\ & \vdots \end{align}$

となり、どちらも 1 から始まる奇数について和を取ることになります。
　1.444-5. 式の場合は、下のグラフのように「奇対称」の位置に配置したものです。

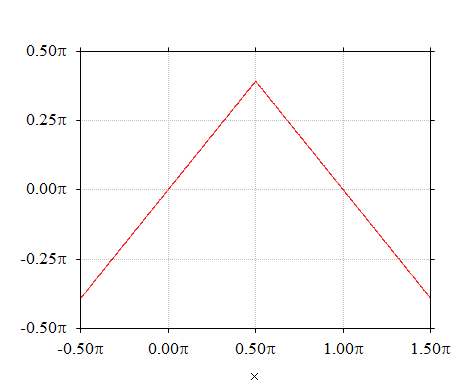
　1.444-6. 式の場合は、下のグラフのように「偶対称」の位置に配置したものです。

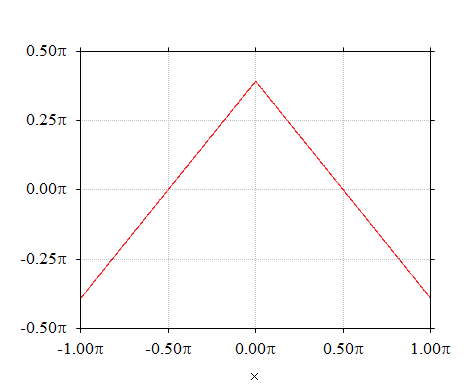
　"Table of Integrals, Series, and Products" には、サイン/コサイン関数を入れ替えた公式は記載されていません。
　そのため、三角波の場合の 90° 位相シフトされた波形については初等関数 (あるいは特殊関数) による表現は不明です。
　ただし、フーリエ級数としては表現できるので、2019 年 3 月 7 日付けの記事のように、値を求めてグラフをプロットすることは可能です。