dsPIC33FJ64GP802 (25) --- 周波数シフター (9)

　前回の三角波のサイン → コサイン置き換え版を、数式処理システムの「Maxima」でフーリエ級数以外の表現で求めてみたところ、やはり、初等関数では表せない形になるようです。
　まず、「方形波」を積分すれば「三角波」になるので、方形波のフーリエ展開の式である 1.442-4. 式の左辺を積分した値を求めると、三角波のフーリエ展開である 1.444-5. 式の左辺、あるいは 1.444-6. 式の左辺に結び付くはずです。
　具体的には、

$\hspace{2em}\displaystyle \begin{align} \int \left( \sum_{k\;=\;1}^\infty \frac{\sin (2k-1) x}{2k-1} \right) dx \end{align}$

を計算することになります。
　積分と級数の和を取る操作との順序は入れ替え可能なので、級数の項別に、まず積分を行うと、

$\hspace{2em}\displaystyle \begin{align} \sum_{k\;=\;1}^\infty \left( \int \frac{\sin (2k-1) x}{2k-1}\ dx \right) = - \sum_{k\;=\;1}^\infty \frac{\cos (2k-1) x}{(2k-1)^2} \end{align}$

となり、これは、符号を除いて三角波のフーリエ展開である 1.444-6. 式の左辺と一致しているのが分かります。
　したがって、方形波のサイン/コサイン入れ替え版である 1.442-2. 式の右辺あるいは 1.442-3. 式の右辺を積分すれば、三角波のサイン/コサイン入れ替え版の関数の形が分かることになります。
　ここでは、逆グーデルマン関数で直接に表される 1.442-3. 式の右辺を対象にします。

$\hspace{2em}\displaystyle \begin{align} \frac{1}{2}\ln \tan \left( \frac{x}{2} + \frac{\pi}{4} \right) = \frac{1}{2}\mathrm{gd}^{-1}\ x \end{align}$

　Maxima の "functs" パッケージには、グーデルマン関数 gd(x) と逆グーデルマン関数 agd(x) が含まれていて、積分を計算することも可能です。　計算してみた結果を下に示します。

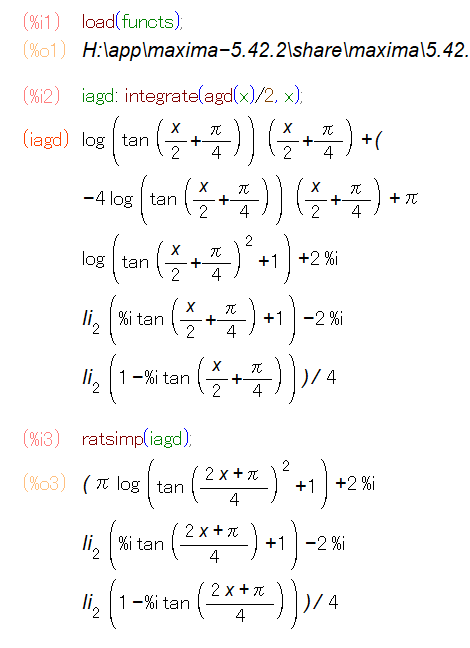
　結果をさらに整理した形で示すと、虚数単位 $i = \sqrt{-1}$ 、複素数の虚部を抜き出す関数を $\mathrm{Im}[\cdot]$ とすると、

$\hspace{2em}\displaystyle \begin{align} \frac{\pi}{4}\ln \left( \tan^2 \left( \frac{x}{2} + \frac{\pi}{4} \right) + 1 \right) - \mathrm{Im} \left[ \mathrm{Li}_2\left( 1 + i\ \tan \left( \frac{x}{2} + \frac{\pi}{4} \right) \right) \right] \end{align}$

となります。
　ここで、 $\mathrm{Li}_2(\cdot)$ は、「多重対数関数」(Polylogarithm) の一種で、「２重対数関数」(dilogarithm) と呼ばれています。
　その定義は、 $z$ を複素数として、

$\hspace{2em}\displaystyle \begin{align} \mathrm{Li}_2(z) = \sum_{k\ =\ 1}^{\infty} \frac{z^k}{k^2} = - \int_{0}^{z}\frac{\ln(1- u)}{u}du \end{align}$

となります。
　級数による表現は、 $|z| \lt 1$ (単位円内) の場合に有効で、単位円外の場合には、上の式の級数を有限項で打ち切ったものをそのまま計算しても値はうまく求まりません。
　多重「対数関数」という名前が付いていますが、対数関数として表すことができる $\mathrm{Li}_1(\cdot )$ を除き、「初等関数」としては扱われません。
　逆グーデルマン関数を積分したものでは、 $\mathrm{Li}_2(\cdot)$ 関数の引き数としては、常に実数部が 1 で、それに虚部が加わったものを計算することになりますから、 $|z| \gt 1$ となり、上の定義通りの級数による計算は有効ではありません。
　数値計算ライブラリ、たとえば GSL (GNU Scientific Library) では、

int gsl_sf_complex_dilog_e(double r, double theta, gsl_sf_result *result_re, gsl_sf_result *result_im)

が用意されており、これを利用すれば簡単に２重対数関数の値を求めることができます。
　log() および tan() は C の math.h に含まれる標準関数を利用し、２重対数関数は GSL の gsl_sf_complex_dilog_e() を利用して、逆グーデルマン関数を積分した式の第１項 (青色のトレース) と第２項 (赤色のトレース) をプロットしたものを下に示します。

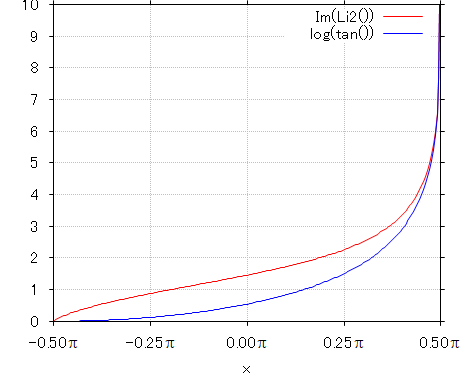
　両者の差、つまり逆グーデルマン関数を積分した式の値そのものをプロットすると、

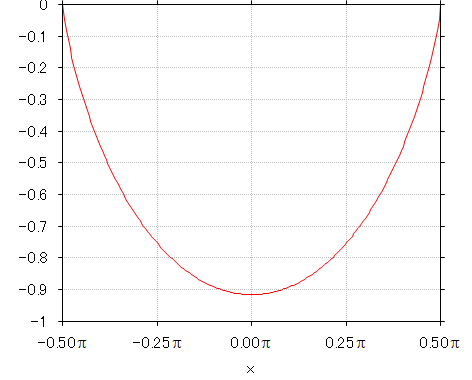
となり、それぞれ左右非対称な項ふたつの差から、左右対称な形が現れます。
　Maxima のグラフ・プロット機能を利用し、

plot2d([iagd], [x, -%pi/2, %pi/2]);

として、Maxima 単体でプロットしたものを下に示します。 (「iagd」は積分結果を格納しておいた変数です)

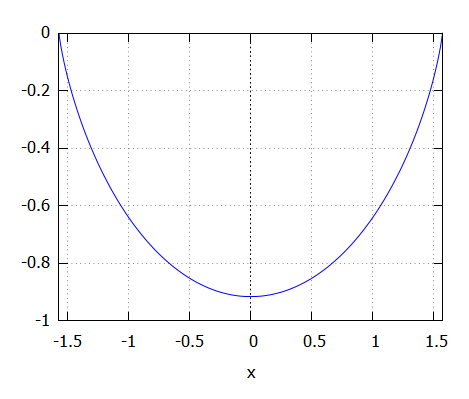
　次回は、逆グーデルマン関数をテイラー展開し、べき級数での表現を求めます。