BBD コーラス (14) -- 逆数特性の VCO (9)

コーラス

前回は、Vx を表す式を積分して時間平均を求めましたが、実は、ほとんど計算らしい計算をせずに時間平均の値を求めることができます。
それは、「定常状態」であれば、コンデンサに流れる電流の時間平均、つまり DC 成分は厳密に「ゼロ」なので、コンデンサはないものとして扱えるからです。
なぜなら、コンデンサ電流の時間平均がゼロではないとすると、どんなに小さな電流であったとしても、時間が経過するにしたがってコンデンサ両端の電位差は増大していき、「定常状態」という前提に矛盾するからです。
ホット側では、定電流源、コンデンサ CL、抵抗 RL だけが接続されており、CL の寄与がないとすれば、定電流源と抵抗 RL だけを考えれば良くなります。
電流 Irew が抵抗 RL に流れれば、電圧降下 Vrew = Irew • RL が発生し、そのデューティー は(Trew/Tcyc) ですから、時間平均を Vave と表すことにすれば、
\qquad\qquad \begin{eqnarray} V_{\mathrm ave} \,=\, \overline{V_{\mathrm x}} &=& V_{\mathrm rew}\,\cdot\, \frac{T_{\mathrm rew}}{\,T_{\mathrm cyc}\,} \\ &=& V_{\mathrm rew}\,\cdot\, T_{\mathrm rew}\,\cdot\, f \end{eqnarray}
となり、前回の結果と一致します。
単に時間平均を求めるだけなら、この計算で十分なのですが、簡易型 V-to-F コンバータの変換誤差の評価のためには、後で示すように、Vbot と Tcyc との間の関係を求める必要があります。
そのため、ちょっと面倒くさい計算をしてきたのです。
前回の式から、さらに計算を進め、Vx のリプル量、つまり、(Vtop - Vbot) を求めると、
\qquad\qquad V_{\mathrm top} \,-\, V_{\mathrm bot} \,=\, (V_{\mathrm rew}\,-\,V_{\mathrm bot})\,\cdot\,(1\,-\,e^{-T_{\mathrm rew}/T_{\mathrm L}})
となります。
Trew、TL いずれも定数なので、後半の、指数関数を含む因子は単に定数となり、この式は、リプル量は Vbot の増加に対してリニアに減少することを示しています。
つまり、リプル量は一定ではなく、Vbot = 0 の場合に最大になり、Vbot = Vrew の場合に最小値ゼロとなることが分かります。
ここで、指数関数の部分をべき級数展開すると、
\qquad\qquad e^{-T_{\mathrm rew}/T_{\mathrm L}}\,=\, 1 \,-\, \frac{T_{\mathrm rew}}{T_{\mathrm L}} \,+\, \frac{1}{2}\cdot \left(\frac{T_{\mathrm rew}}{T_{\mathrm L}} \right)^2 \.-\qquad \cdots
と表されます。
(Trew / TL) << 1 なので、べき級数展開の 2 次以上の項は省略して元の式の指数関数の部分に代入すると、初項の「1」が消し合って 1 次の項だけが残り、
\qquad\qquad V_{\mathrm top} \,-\, V_{\mathrm bot} \,\simeq\, (V_{\mathrm rew}\,-\,V_{\mathrm bot})\,\cdot\,\frac{T_{\mathrm rew}}{T_{\mathrm L}}
と近似できます。
自明なことですが、リプル量を小さくするには、Trew を小さくする方向、TL を大きくする方向に選べばよいことが式で表されました。
さらに、Vbot と Tcyc との関係を計算した結果だけを示すと、
\qquad\qquad V_{\mathrm bot} \,=\, V_{\mathrm rew} \,\cdot\, \frac{1\,-\,e^{-T_{\mathrm rew}/T_{\mathrm L}}}{1\,-\,e^{-T_{\mathrm cyc}/T_{\mathrm L}}}
となります。
これで準備が整いました。
簡易型の V-to-F コンバータの回路を下に示します。

F-to-V コンバータではパルスの整形をするだけだったコンパレータを、負帰還ループの一部として使い、入力電圧に追従させています。
ここで、F-to-V コンバータの出力である Vx のリプルを利用し、「自励式」で発振させています。
Vx の電圧波形の模式的な図を下に再掲し、この図を使って説明します。

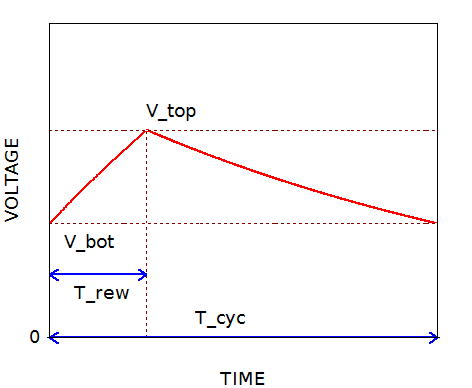
V-to-F コンバータとしての入力電圧 Vin は、コンパレータのプラス入力端子に接続されており、回路動作としては、この図の Vbot がその入力電圧 Vin と一致するようにフィードバックが行われます。
ワンショット期間で、Vtop まで達した Vx は、充電期間が終わって放電期間に入ると電圧が低下してきます。
そして、コンパレータ・スレシホールドであるプラス入力側の電圧を下回るとコンパレータが反転し、ワンショット回路をトリガして、最初の状態へ戻ります。
このようにして、入力電圧 Vin = Vbot となるように動作します。
ここで、もし時間平均 Vave を使うならば、前回および今回見たように、F-to-V コンバータとしては原理的にはリニアリティ誤差が発生しませんが、時間平均して完全に直流にしてしまうと、ループ内に「振動」の要素がどこにも存在せず、「他励式」にしなければ発振器として成立しなくなります。
「簡易型」のはずなのに、他励のための回路の追加が必要になるのはナンセンスですから、「自励式」として、入力電圧 Vin = Vbot となるように動作させます。
そのため、原理的に誤差が発生することになります。
Vbot < Vave < Vtop ですから、誤差を小さくするには、リプル (Vtop-Vbot) を小さくすれば良いのですが、リプルを小さくするというのは、コンパレータ差動入力間の電位差の振幅を小さくすることですから、コンパレータの精度やスピードに影響を与え、出力周波数にジッタが乗ったり、不安定になる可能性があります。
したがって、むやみにリプルを小さくすれば良いというわけではなく、適切な値を選ぶ必要があります。
逆数特性の VCO としての利用では、入力電圧 Vin 固定で、リワインド電流 Irew を変化させますから、Vrew を介してリプル量に影響を及ぼすことになり、出力周波数が高い、つまりリプルが小さい領域で不安定にならないような回路定数を選択する必要があります。
前に示した、Vbot と Tcyc との関係の式で、指数関数の部分をべき級数展開し、2 次以上の項を省略して計算すると、
\qquad\qquad \begin{eqnarray} V_{\mathrm bot} &=& V_{\mathrm rew} \,\cdot\, \frac{1\,-\,e^{-T_{\mathrm rew}/T_{\mathrm L}}}{1\,-\,e^{-T_{\mathrm cyc}/T_{\mathrm L}}} \\ &\simeq& V_{\mathrm rew} \,\cdot\, \frac{T_{\mathrm rew}/T_{\mathrm L}}{T_{\mathrm cyc}/T_{\mathrm L}} \,=\, V_{\mathrm rew} \,\cdot\, \frac{T_{\mathrm rew}}{T_{\mathrm cyc}}\,=\, V_{\mathrm rew} \,\cdot\, T_{\mathrm rew} \,\cdot\, f \end{eqnarray}
となり、exp(-Tcyc/TL) の 1 次の項までを考えるならリニアリティ誤差はなく、誤差としては、この計算では省略した 2 次のオーダーになることが分かります。