BBD コーラス (13) -- 逆数特性の VCO (8)

コーラス

前回は、充電側では t = 0 で電荷ゼロから出発するグラフ、放電側では Vrew までフル充電された状態から出発するグラフを、それぞれ 1 本ずつ書いて、実際の波形は、グラフの一部分を切り取って組み合わせたものとして説明しました。
今回は、t = 0 から Tcyc までの実際の波形を表す式を求め、その 1 サイクル内の時間平均を計算します。
抵抗 RL とコンデンサ CL の「ホット側」(Vx) の波形の概念図を下に再掲します。

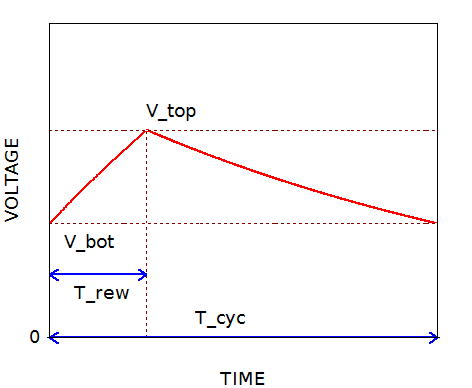
まず、もとの充電側の式
\qquad\qquad V_{\rm x1}(t) \,=\, V_{\rm rew} \,\cdot\, ( 1 \,-\, e^{-t/T_{\rm L}})
の時間の原点 t = 0 を、電圧が Vbot となる点に移動して、再定義します。
\qquad\qquad \begin{eqnarray}V_{\rm x1}(t) &=& V_{\rm rew} \,\cdot\, ( 1 \,-\, e^{-(t+t_{\rm bot})/T_{\rm L}}) \\ &=& V_{\rm rew} \,\cdot\, ( 1 \,-\, e^{-t_{\rm bot}/T_{\rm L}}\,\cdot\,e^{-t/T_{\rm L}})\end{eqnarray}
t = 0 から Trew までは、この式でホット側の電圧が表されることになります。
新しい定義を使うと、Vbot は次のように表されます。
\qquad\qquad \begin{eqnarray} V_{\rm bot} &=& V_{\rm x1}(0)\\ &=& V_{\rm rew} \,\cdot\, ( 1 \,-\, e^{-t_{\rm bot}/T_{\rm L}})\end{eqnarray}
この式を指数関数の部分について解くと、
\qquad\qquad e^{-t_{\rm bot}/T_{\rm L}} \,=\, \frac{V_{\rm rew} \,-\,V_{\rm bot}}{V_{\rm rew}}
この式を新しい Vx1(t) の式に代入すると、
\qquad\qquad V_{\rm x1}(t) \,=\, V_{\rm rew} \,-\, (V_{\rm rew} \,-\,V_{\rm bot}) \,\cdot\,e^{-t/T_{\rm L}}
と表されます。
同様に、放電側のもとの定義
\qquad\qquad V_{\rm x2}(t) = V_{\rm rew} \,\cdot\, e^{-t/T_{\rm L}}
を、t = Tcyc の時点で、Vbot に到達するように書き直すと、
\qquad\qquad V_{\rm x2}(t) = V_{\rm bot} \,\cdot\, e^{-(t-T_{\rm cyc})/T_{\rm L}}
となります。
t = Trew から Tcyc までは、この式でホット側の電圧が表されます。
ホット側の電圧 Vx の時間平均を \overline{V_{\rm x}} とすると、定常状態なので、すべてのサイクルの変化は同等であり、代表して 1 サイクル分 (Tcyc) の時間平均だけを計算すれば良いことになります。
\qquad\qquad \overline{V_{\mathrm x}} = \frac{1}{\,T_{\mathrm cyc}\,} \,\cdot\, \left[ \,\int_0^{\small T_{\mathrm rew}}V_{\mathrm x1}(t)dt \,+\, \int_{\small T_{\mathrm rew}}^{\small T_{\mathrm cyc}}V_{\mathrm x2}(t)dt \,\right]
まず、充電側の定積分の途中の計算は省略して結果だけ示すと、
\qquad\qquad \begin{eqnarray} \int_0^{\small T_{\mathrm rew}}V_{\mathrm x1}(t)dt &=& \left[ V_{\mathrm rew}\cdot t \,+\, (V_{\mathrm rew}-V_{\mathrm bot})\,\cdot\, T_{\mathrm L} \,\cdot\, e^{-t/T_{\mathrm L}} \right]_0^{\small T_{\mathrm rew}} \\ &=& V_{\mathrm rew}\,\cdot\,T_{\mathrm rew}\,-\,(V_{\mathrm top}\,-\,V_{\mathrm bot})\,\cdot\,T_{\mathrm L} \end{eqnarray}
となります。
同様に、放電側の定積分の結果は、
\qquad\qquad \begin{eqnarray} \int_{\small T_{\mathrm rew}}^{\small T_{\mathrm cyc}}V_{\mathrm x2}(t)dt &=& V_{\mathrm bot}\,\cdot\,e^{T_{\mathrm cyc}/T_{\mathrm L}}\,\cdot\,\left[ -T_{\mathrm L}\,\cdot\, e^{-t/T_{\mathrm L}} \right]_{\small T_{\mathrm rew}}^{\small T_{\mathrm cyc}} \\ &=& (V_{\mathrm top}\,-\,V_{\mathrm bot})\,\cdot\,T_{\mathrm L} \end{eqnarray}
となります。
したがって、時間平均は、
\qquad\qquad \begin{eqnarray} \overline{V_{\mathrm x}} &=& \frac{1}{\,T_{\mathrm cyc}\,} \,\cdot\, \left( V_{\mathrm rew}\,\cdot\,T_{\mathrm rew}\,-\,(V_{\mathrm top}\,-\,V_{\mathrm bot})\,\cdot\,T_{\mathrm L} \right) \\ &+& \frac{1}{\,T_{\mathrm cyc}\,} \,\cdot\, (V_{\mathrm top}\,-\,V_{\mathrm bot})\,\cdot\,T_{\mathrm L} \\ &=& V_{\mathrm rew}\,\cdot\, \frac{T_{\mathrm rew}}{\,T_{\mathrm cyc}\,} \\ &=& V_{\mathrm rew}\,\cdot\, T_{\mathrm rew}\,\cdot\, f \end{eqnarray}
となり、自明な結果ですが、平均電圧 \overline{V_{\rm x}} は入力周波数 f に比例することになります。
出力電圧自体は Vbot から Vtop の間を変化しますが、この「リプル量」、つまり (Vtop - Vbot) の大小にかかわらず、平均すれば入力周波数 f に比例した値になります。
この計算では近似は使っていないので、厳密な結果であり、(原理的には) 直線性誤差は生じないことになります。
実際には、定電流出力端子の電圧が変動すると、トランジスタのアーリー効果により出力電流値が変動するので、その分が誤差になります。
カレントミラー部にアーリー効果による誤差が生じると影響が大きくなりますが、LM331 の場合には、電流スイッチ兼カスコード・トランジスタを介して電流出力されているので、影響は少なくなります。
それでも、1 % 以下のリニアリティを求める場合には無視できなくなってきます。