PX-150 (11) - シンセ・アンプラグド

今回は大電流領域で効いてくる２種の誤差の内のひとつを取り上げます。
一般的なリセット式のリニア VCO での誤差の出方については、Franco の補償 (高域補償) と関連して、すでに述べてあります。
SX-150 の方式では、リワインド式と同様に、一定電流を積分コンデンサに注入してリセットしているのですが、リワインド式とは違って、高域で誤差が生じます。
結論として、その量は、一般的なリセット方式での誤差より大きくなります。
まず、ここで使う記号を次のように定義します。

$I_{\rm A}$

アンチログ回路の出力電流 = リニア VCO 部の入力電流

$I_{\rm R}$

リセット期間に積分器に注入する電流

$T_{\rm R}$

リセット期間の幅

$T_{\rm A}$

リニア VCO 入力電流 $I_{\rm A}$ だけを積分している期間の幅

$T_{\rm S}$

リセット時間 $T_{\rm R} = 0$ である、理想のこぎり波の周期

$T^\prime_{\rm S}$

リセット時間 $T_{\rm R}$ の誤差を含む、のこぎり波の実際の周期

$V_{\rm TOP}$

ヒステリシス・コンパレータの上側のスレシホールド電圧 = のこぎり波の上端の電圧 (誤差を含まない理想値)

$V_{\rm BOT}$

ヒステリシス・コンパレータの下側のスレシホールド電圧 = のこぎり波の下端の電圧 (誤差を含まない理想値)

$t_{\rm pdH}$

コンパレータの入力が $V_{\rm TOP}$ を超えてからコンパレータ出力が立ち上がるまでの遅延時間

$t_{\rm pdL}$

コンパレータの入力が $V_{\rm BOT}$ を下回ってからコンパレータ出力が立ち下がるまでの遅延時間

$V^\prime_{\rm TOP}$

伝達遅延 $t_{\rm pdH}$ の間も、のこぎり波の電圧が上昇を続けるため、「行き過ぎる」効果を含んだ実効的な上端のスレシホールド電圧

$V^\prime_{\rm BOT}$

伝達遅延 $t_{\rm pdL}$ の間も、のこぎり波の電圧が下降を続けるため、「行き過ぎる」効果を含んだ実効的な下端のスレシホールド電圧

$C$

積分コンデンサの容量

$f$

誤差を含まない理想発振周波数

$f^\prime$

誤差を含む実際の発振周波数

２種の誤差というのは、

$I_{\rm A}$ の値により、リセット期間の幅が変化することによる誤差
コンパレータの応答時間がゼロでないために生ずる、のこぎり波の振幅が変化することによる誤差

の２つです。
「1.」では、コンパレータは理想的なものとし、伝達遅延はゼロと仮定します。
「2.」では、実際のコンパレータが持つ伝達遅延の影響をスレシホールド・レベルの変化に置き換えて考慮します。
まず、「1.」のリセット期間周辺の図を示します。

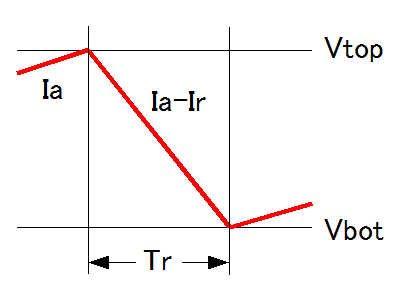
上の図では省略してありますが、まずは、リセット期間以外の、入力電流だけを積分している時間 $T_{\rm A}$ を求めておきます。
これは、のこぎり波/ランプ波形の「緩斜辺」の部分で、下端の電圧 $V_{\rm BOT}$ を出発する時刻をゼロとし、一定の傾斜で上昇して行き、上端の電圧 $V_{\rm TOP}$ に達するまでの時間です。
この期間で容量 $C$ のコンデンサに注入される電荷の量を $\Delta Q$ とすると、コンデンサの端子電圧と電荷の関係式から、
$\qquad \qquad \Delta Q = C \cdot \Delta V = C (V_{\rm TOP} - V_{\rm BOT})$
となります。
この期間 $T_{\rm A}$ の間は一定電流 $I_{\rm A}$ が流れていますから、流入する電流から電荷の量を計算すると、
$\qquad \qquad \Delta Q = I_{\rm A} \cdot T_{\rm A}$
となります。
このふたつの式から、
$\qquad \qquad C (V_{\rm TOP} - V_{\rm BOT}) = I_{\rm A} \cdot T_{\rm A}$
$\qquad \qquad T_{\rm A} = \frac{C (V_{\rm TOP} - V_{\rm BOT})}{I_{\rm A}}$
となります。
理想のこぎり波/ランプ波形ではリセット時間 $T_{\rm R} = 0$ ですから、理想周波数 $f$ は
$\qquad \qquad f = \frac{1}{T_{\rm S}} = \frac{1}{T_{\rm A}} = \frac{I_{\rm A}}{C (V_{\rm TOP} - V_{\rm BOT})}$
となり、入力電流 $I_{\rm A}$ に完全に比例します。
一般的なリセット方式では、リセット時間 $T_{\rm R}$ は定数となり、実際の周波数 $f^\prime$ と理想周波数 $f$ との比は
$\qquad \qquad \frac{f^\prime}{f} = \frac{T_{\rm S}}{T^\prime_{\rm S}} = \frac{T_{\rm A}}{T_{\rm A}+T_{\rm R}} = \frac{1}{1 + T_{\rm R} \cdot f}$
となります。
これは以前の記事 (http://d.hatena.ne.jp/pcm1723/20081114) で書いたものと同じです。
SX-150 の方式では、リセット時間 $T_{\rm R}$ は定数とならず、入力電流 $I_{\rm A}$ により変化します。
先ほどの図を再掲すると、

同様にして、リセット期間の幅 $T_{\rm R}$ を求めると、
$\qquad \qquad T_{\rm R} = \frac{C ( V_{\rm BOT} - V_{\rm TOP})}{I_{\rm A} - I_{\rm R}}$
のこぎり波/ランプ波形の実際の周期 $T^\prime_{\rm S}$ 、実際の周波数 $f^\prime$ を求めると、
$\qquad \qquad \begin{eqnarray}T^\prime_{\rm S} &=& T_{\rm A}+T_{\rm R}=\frac{C (V_{\rm TOP} - V_{\rm BOT})}{I_{\rm A}}+\frac{C ( V_{\rm BOT} - V_{\rm TOP})}{I_{\rm A} - I_{\rm R}}\\ \\&=&C \left( V_{\rm TOP} - V_{\rm BOT} \right)\cdot \left( \frac{I_{\rm R}}{I_{\rm A}(I_{\rm R}-I_{\rm A})}\right)\end{eqnarray}$
$\qquad \qquad \begin{eqnarray} f^\prime &=& \frac{1}{T^\prime_{\rm S}}\\ &=& \frac{I_{\rm A}}{C(V_{\rm TOP} - V_{\rm BOT})}\left( 1 - \frac{I_{\rm A}}{I_{\rm R}} \right) = f \cdot \left( 1 - \frac{I_{\rm A}}{I_{\rm R}} \right)\\ &\,& \\ &=& f \cdot \left( 1 - f \cdot T_{\rm R0} \right)\end{eqnarray}$
となります。
ここで、 $T_{\rm R0}$ は「基本リセット時間」とでも呼ぶべき定数で、その定義は
$\qquad \qquad T_{\rm R0} = \frac{C (V_{\rm TOP} - V_{\rm BOT})}{I_{\rm R}}$
となります。
$T_{\rm R0}$ は、入力電流 $I_{\rm A} \rightarrow 0$ でのリセット時間に相当します。
また、「リセット周波数」とでも呼ぶべき値 $f_0$ を、 $T_{\rm R0}$ の逆数
$\qquad \qquad f_0 = \frac{1}{T_{\rm R0}} = \frac{I_{\rm R}}{C (V_{\rm TOP} - V_{\rm BOT})}$
として定義しておきます。
SX-150 方式の $f^\prime$ の式を見ると、 $f$ の２次式となっていることが分かります。
一般的なリセット方式のリセット時間の表記も $T_{\rm R0}$ 、 $f_0$ に変えてまとめると、

一般的なリセット方式

$\qquad \qquad \qquad \qquad \frac{f^\prime}{f} = \frac{1}{1 + f \cdot T_{\rm R0}}$
$\qquad \qquad \qquad \qquad \frac{f^\prime}{f_0} = \frac{f}{f_0} \, \cdot \, \frac{1}{1 + f / {f_0} }$

SX-150 方式

$\qquad \qquad \qquad \qquad \frac{f^\prime}{f} = 1 - f \cdot T_{\rm R0}$
$\qquad \qquad \qquad \qquad \frac{f^\prime}{f_0} = \frac{f}{f_0} \left (1 - \frac{f}{f_0} \right )$

となります。
横軸に $f/f_0$ 、縦軸に $f^\prime/f_0$ をプロットしてみたのが下の図です。

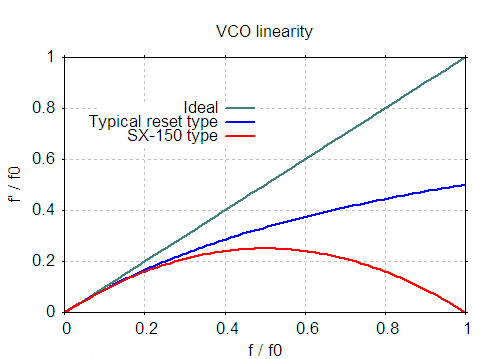
$f/f_0$ が大きくなると直線からズレていきます。
このプロットでは 1.0 までしか示してありませんが、一般的なリセット方式では $f/f_0$ が大きくなると $f^\prime/f_0$ は頭打ちとなり、1.0 に漸近していきます。
SX-150 方式では上に凸な放物線のグラフになり、 ${f/f_0} = 0.5$ で最大値となります。
$f/f_0$ が大きくなるにしたがい、ランプ波形のリセット部分の傾斜がゆるやかになっていき、 ${f/f_0} = 0.5$ で「緩斜辺」と「急斜辺」の傾きが等しくなり、三角波の状態になります。
それ以上 $f/f_0$ ガ増えると、かえって $f^\prime/f_0$ は下がって行き、ランプ波形の「緩斜辺」と「急斜辺」が入れ替わり、ついには ${f/f_{0}} = 1.0$ で周波数が 0 Hz となります。