dsPIC33FJ64GP802 (21) --- 周波数シフター (5)

　以下、(1.441-1.) のような式番号が付けられている式は、

I.S. Gradshteyn, I.M. Ryzhik 著
Alan Jeffrey, Daniel Zwillinger 編
"Table of Integrals, Series, and Products",
Seventh Edition,
Academic Press

からの引用です。
　まずは、のこぎり波のフーリエ展開の式です。

$\displaystyle \begin{align} \sum_{k\; =\;1}^\infty \frac{\sin k x}{k} &= \frac{\pi - x}{2} & [0 < x < 2\pi ] \tag{1.441-1.} \\ \mathstrut \\ \sum_{k\;=\;1}^\infty \frac{\cos k x}{k} &= -\frac{1}{2}\ln\left[2\left(1-\cos x\right)\right] & [0 < x < 2\pi ] \tag{1.441-2.} \end{align}$

　1.441-１. 式の右辺の関数をグラフにすると次のようになります。

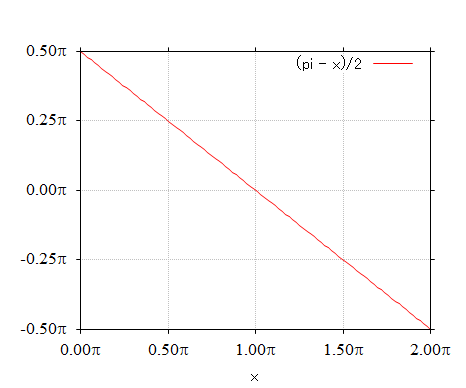
　原点 (0, 0) に対して奇対称になるように配置し、0 から 2 π までを 1 周期とする、右下がりのスロープの (逆) のこぎり波です。
　「奇関数」なので、フーリエ展開のコサイン成分の係数はすべてゼロとなり、

$\displaystyle \begin{align} \qquad\qquad \sum_{k\; =\;1}^\infty \frac{\sin k x}{k} &= \sin x + \frac{1}{2} \sin 2x + \frac{1}{3} \sin 3x + \dots \end{align}$

のようにサイン成分のみが残ります。
　このサイン成分の展開係数をそのままに、サイン関数をコサイン関数に置き換えたのが 1.441-2. 式です。
　サインからコサインへの置き換えは、位相を +90° 進めることに相当します。
　1.441-2. 式の右辺の関数をグラフ化すると次のようになります。

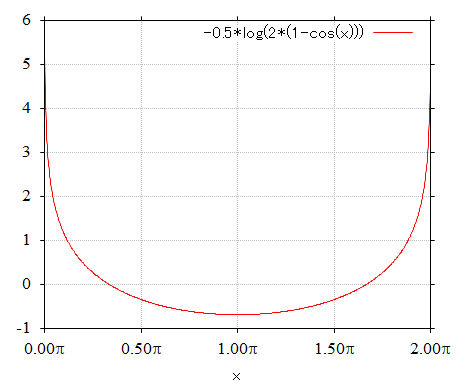
　関数の値は $x = 0$ と $x = 2 \pi$ で無限大になりますが、グラフのプロットからは省いてあります。
　前回のヒルベルト変換器出力の場合と同じ、正方向に鋭いピークを持つ波形となっていますが、これは、

のこぎり波の形状は前回は右上がり、今回は右下がりで符号が逆。
ヒルベルト変換器出力の位相差は -90° で、サイン→コサインの置き換えでは +90° で符号が逆。

となっており、マイナスかけるマイナスでプラスとなり、極性が一致していることになります。
　1.441.-2. 式の左辺のフーリエ級数の和を第 79 次高調波成分までで打ち切ったものと、右辺の関数の値との差、つまり、フーリエ級数の打ち切り誤差をグラフにしたものを下に示します。

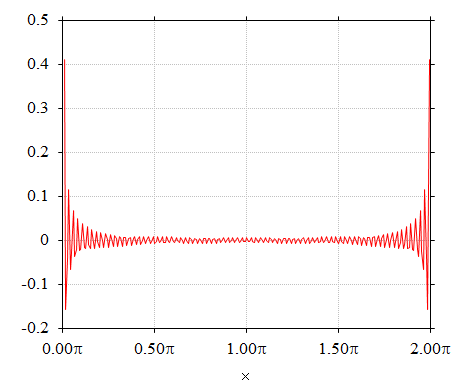
　右上がりのスロープを持つのこぎり波の場合を下に示します。

$\hspace{-1em}\displaystyle \begin{align} \sum_{k\;=\;1}^\infty \frac{(-1)^{k-1}\sin k x}{k} & = \frac{x}{2} & [-\pi < x < \pi ] \tag{1.441-3.} \\ \mathstrut \\ \sum_{k\;=\;1}^\infty (-1)^{k-1}\frac{\cos k x}{k} & = \ln\left(2 \cos\frac{x}{2}\right) & [-\pi < x < \pi ] \tag{1.441-4.} \end{align}$

　1.441-3. 式の右辺の関数のグラフを次に示します。

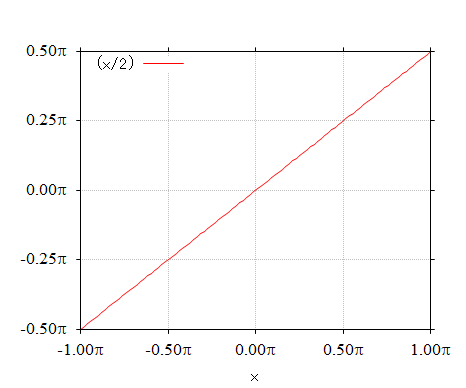
　右上がりのスロープの中央を原点 (0, 0) に配置して「奇関数」としてコサイン成分をゼロにしています。　のこぎり波の場合、「偶関数」となるような配置はできません。
　このフーリエ展開は、左辺のように、係数の符号がプラス/マイナス交番する形となります。
　展開係数をそのままに、サイン関数からコサイン関数に置き換えたのが 1.441-4. 式です。
　1.441-4. 式の右辺の関数のグラフを下に示します。

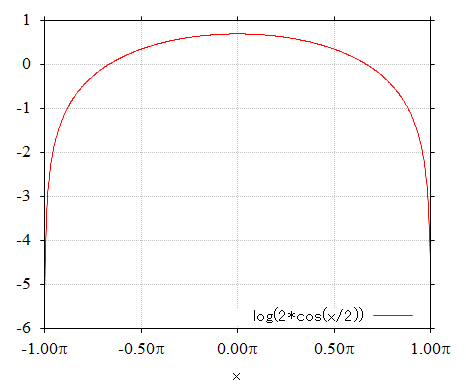
　のこぎり波は右上がりで 1.441-1. 式とは符号が逆なので、下向きにピークを持つ波形となっています。
　1.441-2. 式の右辺の関数と、1.441-4. 式の右辺の関数とは、一見して違いがあるように見えますが、三角関数の半角の公式より、1.441-2. 式の右辺は、

$\displaystyle\begin{align} \qquad\qquad - \frac{1}{2} \ln \left[ 2 \left( 1 - \cos x\right ) \right] &= - \frac{1}{2} \ln \left( 4 \sin^2 \frac{x}{2}\right ) \\ &= - \ln \left( 2 \sin \frac{x}{2}\right ) & \left[ 0 < x < 2\pi \right] \end{align}$

となり、1.441-2. 式と符号 (波形の極性) および位相のみ異なることが分かります。
　次回は、方形波の場合について触れます。