dsPIC33FJ64GP802 (27) --- 周波数シフター (11)
2019 年 3 月 24 日付けの記事では、方形波を表すフーリエ級数表現の式を積分して、三角波のフーリエ級数表現が得られることを示しましたが、サイン/コサイン入れ替え版の式は求めていませんでした。
1.442-3. 式の左辺の積分を計算すると次のようになります。
(2019 年 3 月 31 日追記:以下、項目だけではなく具体的な式の形も併記しました)
これで、
の 3 種の表現が求まったので、その 3 つを重ねてプロットしてみました。

緑色のトレースがフーリエ級数近似 (15 次高調波までを加算)、青色のトレースがべき級数近似 (24 次の項まで加算)、赤色のトレースが agd(x) の積分結果による表現です。
フーリエ級数近似と agd(x) の積分結果による表現との差のグラフを下に示します。
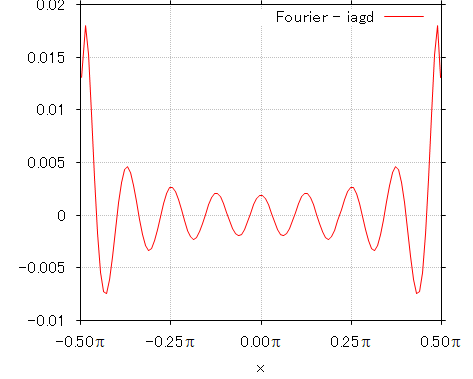
「誤差」は全体に振動的に表れていますが、 および
の周辺で正側に大きく出ており、テイラー展開の場合と逆方向になっています。
三角波をヒルベルト変換器に通すとこの「太ったサイン波」状の波形が得られるのですから、逆に「太ったサイン波」波形をヒルベルト変換器に入力すると三角波が出力に得られることになります。
上記の 3 種類の表現を数値計算して wave ファイルを作成し、WaveGene のユーザ波形再生機能を利用してヒルベルト変換器に入力してみました。
フーリエ展開では三角関数の周期性により全周期で有効ですが、べき級数近似および agd(x) の積分結果による式では、 の範囲でしか有効ではないので、
の範囲については符号を反転して繰り返すことにより 1 周期分の波形を構成しています。
まずは、agd(x) の積分結果の表現の場合です。

上側の波形がヒルベルト変換器への入力で、下側の波形がヒルベルト変換器からの出力です。
最も正確な表現なので、きれいな三角波が得られています。
次は、べき級数近似の場合です。
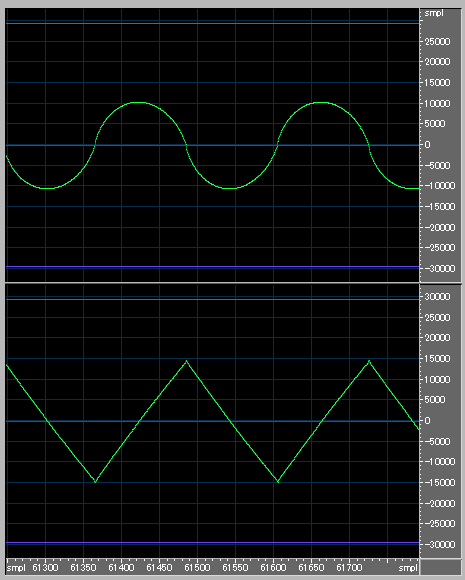
この大きさのプロットでは見にくいのですが、三角波の頂点がすこし尖って飛び出しています。
最後にフーリエ級数近似の場合です。
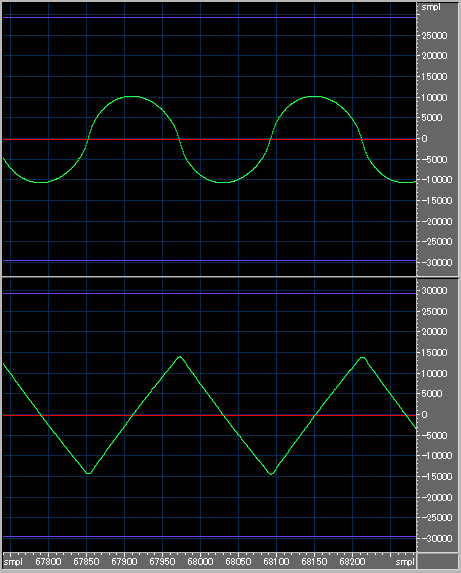
三角波の頂点がすこし凹んだようになっています。
理論的には当然なのですが、ずんぐりむっくりした「太ったサイン波」をヒルベルト変換器に入力して、出力から「シュッ」とした三角波が得られるのは面白いです。