dsPIC33FJ64GP802 (28) --- 周波数シフター (12)

　現状の周波数シフター・プログラム (2019 年 2 月 7 日付けの記事に hex ファイルを掲載) では、処理に余裕があったので、 2019 年 1 月 16 日付けの記事の実質 507 タップのヒルベルト変換器ではなく、タップ数を増やして実質 763 タップとしたものを使っています。
　GNU Octave による設計プログラムをまだ掲載していなかったので、下に示します。

# load "signal" package
pkg load signal;
# 382 tap FIR filter for Hilbert transform
N_tap = 382;
# sampling frequency
f_s = 24000;
# passband lower edge frequency
f_0 = 70;
# passband gain
gain = 1.0;
# weight
weight = 1;
# plot points
N_plot = 1024;
# Parks-McClellan optimal FIR filter design
hb = remez(N_tap-1, [f_0/(f_s/2), 1.0], [gain, gain], [weight], "hilbert");
# frequency plot
freqz(hb, 1, N_plot, f_s);
# output filter coefficients
fid = fopen("hilb382_70Hz.txt", "wt");
fprintf(fid, "// Hilbert transformer coefficients\n");
fprintf(fid, "// use with \"FIRHilbert()\" function\n");
fprintf(fid, "// N_tap = %d\n", N_tap);
fprintf(fid, "// fs    = %.3f kHz\n", (f_s/1000.0));
fprintf(fid, "// fc    = %.3f Hz\n", f_0);
fprintf(fid, "#define Hilb_taps (2*%d - 1)\n", N_tap);
fprintf(fid, "// first half of coefficients (imaginary part of analytic signal)\n");
fprintf(fid, "  Q15(%g),  \n", hb(1:(N_tap/2)));
fprintf(fid, "// center tap (real part of analytic signal)\n");
fprintf(fid, "  Q15( %#g)\n", 1.0);
fclose(fid);

　タップ数が増えたことにより、通過域下端の周波数が 70 Hz、通過域リプルが約 0.1 dB を実現できています。
　通過域の周波数応答を拡大してプロットしたものを下に示します。

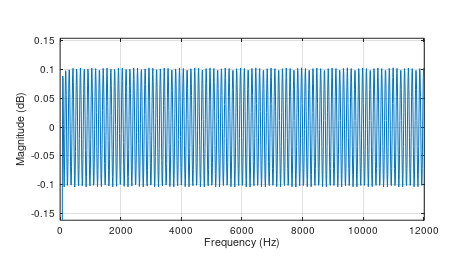
　ヒルベルト変換器の「性能」を測定してみました。
　周波数シフト量を 500 Hz、WaveGene で発生させる正弦波の周波数を 500 Hz → 1500 Hz のリニアスイープとして周波数シフタに入力し、WaveSpectra のピーク・ホールドモードで観測したものです。　(図をクリックすると拡大します)

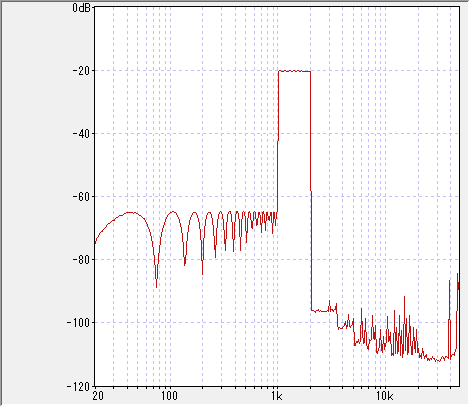
　本来の目的の (プラス方向の) 周波数シフトでは、(500 Hz + 500 Hz) = 1000 Hz から、(500 Hz + 1500 Hz) = 1500 Hz までの正弦波が出力されます。
　図で 1 kHz から 1.5 kHz の、-20 dB の目盛りの線の上にプロットされているのが、この本来の目的の成分です。
　ヒルベルト変換器のゲイン特性が完全に「1」の理想特性ではなく、実際には「リプル」があるため、不要成分である「差周波数」の成分が生じています。
　その周波数は、(500 Hz - 500 Hz) = 0 Hz から (1500 Hz - 500 Hz) = 1000 Hz で、図では 20 Hz から 1000 Hz までの -60 dB 以下のレベルでリプルを伴ったプロットとして表示されています。
　「最小減衰量」としては -45 dB 程度で、この後で示す理論値の -44.7 dB とほぼ一致しています。
　解析信号 (analytical signal) を作り出す元となる正弦波の角周波数を $\omega_\mathrm{A}$ 、ヒルベルト変換器のゲインの 1 からの偏差 (リニア値) を $r$ 、90° ( $\pi/2$ ) 移相からの偏差を $\theta$ [rad]、振幅は簡単のため「1」とすると、この誤差要因を含む解析信号は、

$\hspace{0em}\begin{align} \displaystyle \cos(\omega_\mathrm{A}t) + i \cdot (1 + r) \sin(\omega_\mathrm{A}t+\theta) \end{align}$

となります。
　ヒルベルト変換器のディジタル実現では、フィルタ係数の対称性により、原理的に位相差はリプル等を含まず正確に 90° ですが、ここでは一般的に位相の偏差の項も入れておきます。
　周波数シフトのためのキャリアの角周波数を $\omega_\mathrm{C}$ とすると、周波数シフト操作は、

$\hspace{0em}\begin{align} \displaystyle & \ e^{i \omega_\mathrm{C}t} \cdot {\large(} \cos(\omega_\mathrm{A}t) + i \cdot (1 + r) \sin(\omega_\mathrm{A}t+\theta) {\large)} \\ = & \ e^{i \omega_\mathrm{C}t} \cdot {\large(} \cos(\omega_\mathrm{A}t) + i \cdot (1 + r) (\sin(\omega_\mathrm{A}t)\cos(\theta) + \sin(\theta)\cos(\omega_\mathrm{A}t)) {\large)} \\ \doteqdot & \ e^{i \omega_\mathrm{C}t} \cdot {\large(} \cos(\omega_\mathrm{A}t) + i \cdot (1 + r) (\sin(\omega_\mathrm{A}t) + \theta\cos(\omega_\mathrm{A}t)) {\large)} \end{align}$

と表せます。
　ここで、位相誤差は十分小さい $(\theta \ll 1)$ として、 $\cos(\theta) \doteqdot 1$ 、 $\sin(\theta) \doteqdot \theta$ と近似しました。
　さらに計算を進めると、次のように、角周波数和成分の項と角周波数差成分の項との和として表せます。

$\hspace{0em}\begin{align} \displaystyle & \ \left( 1 + \frac{r}{2} + i\frac{\theta}{2} \right) e^{(\omega_\mathrm{C} + \omega_\mathrm{A})t} - \left( \frac{r}{2} - i\frac{\theta}{2} \right) e^{(\omega_\mathrm{C} - \omega_\mathrm{A})t} \\ \doteqdot & \ e^{(\omega_\mathrm{C} + \omega_\mathrm{A})t} - \left( \frac{r}{2} - i\frac{\theta}{2} \right) e^{(\omega_\mathrm{C} - \omega_\mathrm{A})t} \end{align}$

　ここで、 $r$ も $\theta$ も十分小さいとして、 $(1 + r/2 + i\cdot \theta/2) \doteqdot 1$ と近似しています。
　和成分の振幅を「1」と近似したので、差成分の振幅は

$\hspace{0em}\begin{align} \displaystyle \left| \frac{r}{2} - i\frac{\theta}{2} \right| = \frac{1}{2}\sqrt{\mathstrut r^2 + \theta^2} \end{align}$

で求められます。
　 $\delta$ を dB 単位でのリプルの値、 $\theta$ を度単位での位相誤差とし、差成分の振幅を dB 表現で求めると、

$\hspace{-0.5em}\begin{align} \displaystyle \textrm{Sideband Suppression [dB]} = 10 \cdot \log_{10}\left( (10^{\delta/20}-1)^2 + \left(\frac{\pi \cdot \theta}{180}\right)^2 \right) - 6.0206 \end{align}$

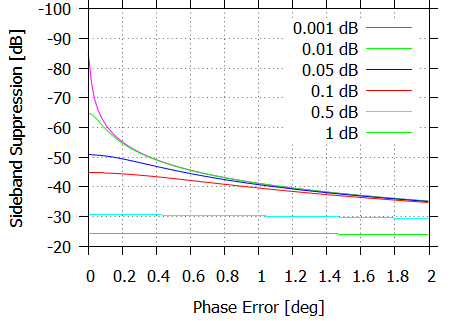
　dB 単位のリプルをパラメタとして、この式の値をプロットしたものを下に示します。

　 $\theta = 0$ 、 $\delta = 0.1$ [dB] での具体的な値は -44.7 dB となります。
　-60 dB を超えるような抑圧比を得るためには、リプルをもう 1 桁減らして、0.01 dB 程度にしなければならないことが分かります。