4 次 VCF CEM3320/V3320 (18) --- 4 次 APF (2) - シンセ・アンプラグド

　データシート記載の 4 次 APF の回路を書き直したものを下に示します。　(図をクリックすると拡大します。)

　フィードバックは LPF 側にしか入っていないので、「正しくないフィードバック」となっています。
　この 4 次 APF 回路の、信号に注目したブロック・ダイアグラムを下に示します。

　下図のような一般的なシステムを考えると、

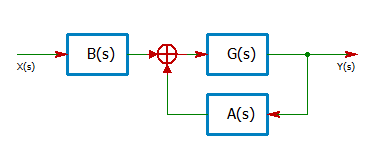
　その伝達関数 F(s) は、

$\qquad\qquad\displaystyle F(s) = \frac{Y(s)}{X(s)} = \frac{B(s)}{(1/G(s)) - A(s)}$

と表されます。
　データシートの回路では、

$\qquad\qquad\displaystyle \left\{ \begin{eqnarray} B(s) &=&\frac{s-1}{s+1} \\ G(s) &=& \left( \frac{s-1}{s+1}\right)^3 \\ A(s) &=& \frac{A}{s+1} \end{eqnarray} \right.$

ですから、これらを代入すると、伝達関数 F(s) は、

$\quad\displaystyle F(s) = \frac{B(s)}{(1/G(s)) - A(s)} = \frac{s-1}{\frac{(s+1)^4}{(s-1)^3} -A} = \frac{(s-1)^4}{(s+1)^4 - A\cdot(s-1)^3}$

と求められます。　
　フィードバック・ゲインである A を -0.9 から 0.9 まで変化させながら振幅の周波数特性をプロットすると、

のようになります。　
　ここで、フィードバック・ゲイン A の値が負の場合は、フィードバックが「正帰還」になることを示しています。
　フィードバックは 1 次 LPF を介して導入されるので、LPF の減衰域である正規化角周波数 1 以上の領域では周波数が高くなるにつれてフィードバック量が少なくなり、裸の特性であるゲイン 0 dB に近付いていきます。
　位相の周波数特性のプロットを下に示します。

　4 次 APF では、位相が 0° から 720° まで回るのに対し、グラフでは ±180° までしか表現できないので、途中で -180° から 180° までのジャンプが 2 回生じていて見にくくなっています。
　位相が約 -205°、-410°、-620° の点が「ピン止め」されていて、フィードバック・ゲイン A の値によらず変化しません。　位相特性が変化できるのはピン止めされた点の間だけなので、小幅なものにとどまっています。
　このデータシート記載の 4 次 APF 構成の回路の LTspice シミュレーション記述を下に示します。

　FCIN = 70.9mV としてカットオフ周波数を固定し、フィードバック・ゲイン A を -0.9 から 0.9 までステッピングさせてシミュレーションしています。
　AC 解析の結果の振幅特性 (上側) と位相特性 (下側) のグラフを下に示します。

　フィードバック・ゲイン A と、トレースの色との対応表を示します。

A	トレースの色
-0.9	赤
-0.5	青
0.0	緑
0.5	マゼンタ
0.9	シアン

　LTspice の機能で、360° を超える範囲も連続的にプロットされているので、位相特性が見やすくなっています。
　位相が約 -205°、-410°、-620° の点が「ピン止め」されていて、位相特性が大きく変化できなくなっているのが分かります。