アナログシンセの VCO ブロック (53) -- マルチ出力アンチログ回路の測定 (3)

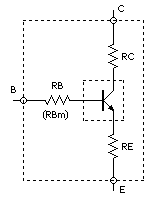
Spice の Ebers-Moll モデルでは、バイポーラ・トランジスタが大電流領域において理想 PN 接合の特性からズレてくる効果を、理想 PN 接合による「真性トランジスタ」の外部に直列抵抗を接続することにより表現しています。
直列抵抗の「実体」としては、端子のリードフレーム/ボンディング・ワイヤ/メタル配線や、(PN 接合部ではない) 半導体のバルク抵抗などです。
左の図のように、内側の破線で囲った部分を理想 PN 接合特性の真性トランジスタ部分として、そのベース、エミッタ、コレクタにそれぞれ「オーミック」(Ohmic) つまりオームの法則にしたがう「普通」の抵抗を直列に接続したものをシミュレーション上のトランジスタのモデルとしています。
実際には、Spice では「改良型」である Gummel-Poon モデルを主に使用しますが、その場合でもエミッタ直列抵抗 R_E とコレクタ直列抵抗 R_C は受け継がれ、ベース直列抵抗は 2 分割されて「外部抵抗」 R_Bm とモデル内部で使われるベース抵抗に分けられます。
この外部直列抵抗による影響としては、エミッタ抵抗 R_E では、エミッタ電流 I_E により抵抗両端に (I_E · R_E) だけの電圧降下が生じ、トランジスタ・モデルの BE 端子間に加えられる電圧 V_BE から、この電圧降下分だけ目減りした電圧が内部の真性トランジスタの BE 端子間に加わることになります。
同様にして、ベース直列抵抗 R_B (R_Bm) についても (I_BE · R_B) の電圧降下が生じます。
このエミッタ抵抗 R_E とベース抵抗 R_B による影響は直流電流増幅率 h_FE (β_F) を媒介として相互に変換可能で、
$\qquad\qquad R_{\rm B} = (1\, +\, h_{\rm FE})\, \cdot\, R_{\rm E}$
$\qquad\qquad R_{\rm E} = R_{\rm B} /(1\, +\, h_{\rm FE})$
となります。
ベース抵抗 R_E、エミッタ抵抗 R_B ともに存在する場合に、ベース抵抗 R_B = 0 として R_B の寄与をエミッタ抵抗 R_E 側に取り込んだ値を R_E^′ とすると、
$\qquad\qquad R_{\rm E}^\prime = R_{\rm E} \,+\, R_{\rm B} /(1\, +\, h_{\rm FE})$
となります。 (ここではプライム記号「′」は「微分」の意味ではありません)

このようにして、ベース抵抗、エミッタ抵抗の寄与を全てエミッタ抵抗側に集めてベース抵抗 R_B = 0 とした場合の、典型的なアンチログ回路を左に示します。
この図で、トランジスタは理想的な真性トランジスタを表すものとし、コレクタ直列抵抗 R_C は回路動作には影響しないのでゼロとしています。
まず、Q1 側の
I_C1 = I_ref = V_ref / R_ref
に対する式を立てると、

$\qquad\qquad I_{\rm C1} \,=\, I_{\rm ref} \,=\, I_{\rm S}\,\cdot\, \exp\left[\frac{q}{kT}\left( -V_{\rm E} \,-\, I_{\rm ref} \,\cdot\, R_{\rm E1}^\prime \right)\right]$
となります。
ここで具体的な値を求めると、R_E は 1 Ω 程度、I_ref については、アンチログ出力電流のレンジを 1 μA 〜 1 mA としてその相乗平均の 32 μA 程度に選ぶとすると、エミッタ抵抗 R_E1^′ による電圧降下は
I_ref · R_E1^′ = 32 [μA] · 1 [Ω] = 32 μV
となり、半音 (100 セント) に対する電圧が約 1.5 mV ということから計算すると 32 μV は約 2 セントの誤差にしかならないので、簡単のため R_E1^′ による誤差は無視して、
$\qquad\qquad I_{\rm ref} \,=\, I_{\rm S}\,\cdot\, \exp\left[\frac{q}{kT}\left( -V_{\rm E} \right)\right]$
とします。
Q2 側のアンチログ出力電流 I_out^′ に対する式を立てると、
$\qquad\qquad I_{\rm out}^\prime \,=\, I_{\rm S}\,\cdot\, \exp\left[\frac{q}{kT}\left( V_{\rm in} \,-\, V_{\rm E} \,-\, I_{\rm out}^\prime \,\cdot\, R_{\rm E2}^\prime \right)\right]$
となります。　これに先の I_ref の式を代入すると、
$\qquad\qquad I_{\rm out}^\prime \,=\, I_{\rm ref}\,\cdot\, \exp\left[\frac{q}{kT}\left( V_{\rm in} \,-\, I_{\rm out}^\prime \,\cdot\, R_{\rm E2}^\prime \right)\right]$
となります。
エミッタ直列抵抗 R_E2 = 0、つまり誤差を含まない理想特性を I_out とすると、
$\qquad\qquad I_{\rm out} \,=\, I_{\rm ref}\,\cdot\, \exp\left[\frac{q}{kT}\left( V_{\rm in} \right)\right]$
となり、両者の比をとると、
$\qquad\qquad \frac{\,I_{\rm out}^\prime\,}{I_{\rm out}} \,=\, \exp\left[\frac{q}{kT}\left( -I_{\rm out}^\prime \,\cdot\, R_{\rm E2}^\prime \right)\right]$
と表されます。
この式から、アンチログ出力誤差がエミッタ直列抵抗によるものと仮定した場合の直列抵抗値の概算値を測定結果から求めてみると、

MIDI ノート・ナンバー最大値でコレクタ電流は約 1 mA
出力誤差は約 -50 セントで、アンチログ入力電圧換算で約 0.75 mV

から、
0.75 [mV] = I_out^′ · R_E2^′ = 1 [mA] · R_E2^′
R_E2^′ = 0.75 [Ω]
となります。
I_out^′ の比の式での指数関数をテイラー展開すると、
$\qquad\qquad \begin{eqnarray}\frac{\,I_{\rm out}^\prime\,}{I_{\rm out}} \,&=&\, \exp\left[\frac{q}{kT}\left( -I_{\rm out}^\prime \,\cdot\, R_{\rm E2}^\prime \right)\right]\\&=& 1 \,/\, \left[1 \,+\, \frac{q}{kT}\left( I_{\rm out}^\prime \,\cdot\, R_{\rm E2}^\prime \right) \,+\, \frac{1}{2} \left{\frac{q}{kT}\left( I_{\rm out}^\prime \,\cdot\, R_{\rm E2}^\prime \right)\right}^2 \,+\, \cdots \right]\end{eqnarray}$
と表されます。
これを 2 次以上の項は無視して、1 次の項までで打ち切ると、以前に求めたリセット型 VCO でのリセット時間に起因する誤差、およびベース結合型アンチログ回路でのベース電流に起因する誤差の式 (以前の記事 → こちら)
$\qquad\qquad \frac{f^\prime}{f} = \frac{1}{1 + T_{\rm R} \cdot f}$
と同じ形になります。 (f^′ と f との差が小さいとして)
アンチログ出力誤差の出方を近似するふたつのモデル

リセット時間誤差近似 (下図の青いプロット)
エミッタ直列抵抗誤差近似 (下図の赤いプロット)

での誤差カーブと、実際の測定データとを比較した近似誤差をプロットしたのが下の図です。

リセット時間誤差近似については全域で近似誤差が小さい状態にはできないので、MIDI ノート・ナンバー 1 から 100 までの測定データに対してフィッティングしたもので、エミッタ直列抵抗誤差近似に対しては MIDI ノート・ナンバー 1 から 127 までの測定データを使ってフィッティングしたものです。
エミッタ直列抵抗誤差近似では、全域に渡り 1 セント以下の近似誤差で測定データの誤差の出方を「説明」できていることが分かります。
リセット時間誤差近似にしても、約 8 オクターブ分は近似誤差は小さく、最大の近似誤差でも 5 セント程度となっています。
リセット型 VCO のリセット時間誤差は Franco の補償により抵抗 1 本で簡単に補正できるので、現在未実装のもう 1 系統のアンチログ出力にはリセット型 VCO を実装して、Franco の補償でどこまで誤差を少なくできるかを試してみようと思っています。