3.3 V ノイズジェネレータ (4) - シンセ・アンプラグド

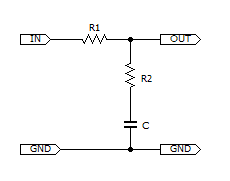
今回は、左の図のようなラグ・リード・フィルタで、中心周波数付近でゲインのスロープが -3 dB/oct (-10 dB/dec) になる条件を求めてみます。
まず、時定数を
$\qquad\qquad T_1 = R_1 \cdot C$
$\qquad\qquad T_2 = R_2 \cdot C$
とすると、この回路の伝達関数は、
$\qquad\qquad H(s) = \frac{s \cdot T_2 + 1}{s\cdot(T_1 + T_2) + 1}$
と表されます。
虚数単位を ${\rm i} = \sqrt{-1}$ 、角周波数を $\omega$ として、 $s = i\cdot \omega$ と置き、伝達関数の絶対値２乗を求めると、
$\qquad\qquad \begin{eqnarray}\left|\, H({\rm i}\cdot \omega)\, \right|^2 &=& \frac{\omega^2 \, T_2^2 \,+ \,1}{\omega^2 \, (T_1 + T_2)^2 \,+\, 1}\\&\quad&\\&=&\frac{T_2}{T_1\,+\,T_2} \cdot \frac{(\omega T_2)^{-1}\,+\,\omega T_2}{\left( \omega (T_1\,+\,T_2) \right)^{-1}\,+\,\omega(T_1\,+\,T_2)}\end{eqnarray}$
となります。
最後の式で $(\,\cdot\,)^{-1}$ を使った形に変形してあるのは、後での計算の都合によるものです。
ここで、コンデンサの値 C は、規準化素子値として $C = 1$ と置き、実際に使う (角) 周波数へは「周波数スケーリング」によって変換するものとします。
したがって、時定数 $T_1 = R_1$ 、 $T_2 = R_2$ と表記でき、式からは表面上 $C$ が消えます。
また、 $R_2\, < \,1$ として $R_1$ と $R_2$ の間に
$\qquad\qquad R_2 = \frac{1}{R_1\,+\,R_2}$
の関係を仮定します。
これは、中心角周波数を 1 [rad/s] に設定する操作であり、こうしても一般性を損ないません。
$R_1$ は
$\qquad\qquad R_1 = \frac{1}{R_2}\,-\,R_2$
で求まり、絶対値２乗の式から $R_1$ の表記を消すことができます。
これらの条件のもとで絶対値２乗の式を書き直すと、
$\qquad\qquad \left|\, H({\rm i}\cdot \omega)\, \right|^2 =R_2^2 \,\cdot\, \frac{(\omega R_2)^{-1}\,+\,\omega R_2}{\left( \omega / R_2 \right)^{-1}\,+\,(\omega / R_2)$
となります。
(角) 周波数特性を対数目盛りのグラフで描くことを考え、(角) 周波数軸 (x 軸) 上の原点からのリニアな座標位置を $x$ で表現して、角周波数 $\omega$ を
$\qquad\qquad \omega = 10^{x} = e^{x\cdot \ln(10)}$
で表記します。　ここで、 $\ln(\,\cdot\,)$ は自然対数 $\log_e(\,\cdot\,)$ を表すものとします。
いくつかの $x$ の値について $\omega$ の値を示すと、
$\qquad\qquad x = -1, \qquad\qquad\qquad \omega = 10 ^{-1} = 0.1$
$\qquad\qquad x = 0, \qquad\qquad\qquad \omega = 10 ^{0} = 1$
$\qquad\qquad x = 1, \qquad\qquad\qquad \omega = 10 ^{1} = 10$
となります。 $x$ が 1 増えれば $\omega$ は 10 倍に、つまり 1 ディケード変化します。
ここで、 $\omega$ を含む項について計算しておきます。
$\qquad\qquad \omega R_2 = e^{x\cdot \ln(10)}\,\cdot\,e^{\ln(R_2)}=e^{x\cdot \ln(10) + \ln(R_2)}$
$\qquad\qquad \omega / R_2 = e^{x\cdot \ln(10)}\, /\,e^{\ln(R_2)}=e^{x\cdot \ln(10) - \ln(R_2)}$
これを絶対値２乗の式に代入すると、
$\qquad\qquad \begin{eqnarray}\left|\, H({\rm i}\cdot 10^x)\, \right|^2 &=& R_2^2 \,\cdot\, \frac{e^{-\left(x \cdot \ln(10) + \ln(R_2)\right)}\, +\, e^{x \cdot \ln(10) + \ln(R_2)}}{e^{-\left(x \cdot \ln(10) - \ln(R_2)\right)}\, +\, e^{x \cdot \ln(10) - \ln(R_2)}}\\ &\quad&\\&=& R_2^2 \,\cdot\, \frac{\cosh\left(x\cdot\ln(10)\,+\,\ln(R_2)\right)}{\cosh\left(x\cdot\ln(10)\,-\,\ln(R_2)\right)}\end{eqnarray}$
となります。　ここで、 $\cosh(\,\cdot\,)$ は双曲線余弦 (hyperbolic cosine) 関数で、
$\qquad\qquad \cosh(x) = \frac{e^x + e^{-x}}{2}$
で定義されます。
さらに、ゲインを dB 単位で表示するために、絶対値２乗の式の常用対数を取ります。
常用対数を取ったあとにかける係数は、絶対値２乗なので「20」ではなく「10」であることに注意して、ゲインを $G(x)$ と表すことにすると、
$\qquad\qquad \begin{eqnarray} G(x) &=& 10 \cdot \log_{10} \left\{ \left| H(10^x) \right|^2 \right\} \\ &\quad& \\ &=& 10 \cdot \log_{10} \left\{ R_2^2 \cdot \frac{\cosh\left(x\cdot\ln(10)\,+\,\ln(R_2)\right)}{\cosh\left(x\cdot\ln(10)\,-\,\ln(R_2)\right)}\right\} \\ &\quad& \\ &=& 20 \cdot \log_{10}(R_2)\,+\,10\cdot\log_{10}\left\{\cosh\left(x\cdot\ln(10)+\ln(R_2)\right)\right\}\\ &\quad& \\ &\quad& \,-\,10\cdot\log_{10}\left\{\cosh\left(x\cdot\ln(10)+\ln(R_2)\right)\right\}\\ &\quad& \\ &=& 20 \cdot \log_{10}(R_2)\,+\,\frac{10}{\ln(10)}\left\{\ln\left[\cosh\left(x\cdot\ln(10)+\ln(R_2)\right)\right]\\ &\quad& \\ &\quad& \,-\,\left.\ln\left[\cosh\left(x\cdot\ln(10)-\ln(R_2)\right)\right]\right\}\end{eqnarray}$
ここまで、ちょっと長かったですが、これで準備が整いました。
このゲインの式を $x$ で微分して勾配を求めると、その数値の単位は [dB/dec] になります。
なぜなら、 $x$ の単位長さ当たり角周波数は 10 倍、つまり 1 ディケード変化するので、分母側のディメンションは「dec」になり、ゲインは dB 単位で表示していますから、当然、分子側のディメンションは「dB」になります。
したがって、 $G(x)$ を $x$ で微分した微係数 $G^\prime(x) = -10$ と置けば、ゲインの勾配が -10 dB/dec (-3 dB/oct) になる条件を求めることができます。
まず、ゲインの式を $x$ で微分すると、
$\qquad\qquad \begin{eqnarray}G^\prime(x) &=& \frac{10}{\ln(10)} \left\{ \ln(10)\cdot \tanh\left[ x\cdot \ln(10) + \ln(R_2)\right]\right\}\\ &\quad&\\ && -\frac{10}{\ln(10)} \left\{ \ln(10)\cdot \tanh\left[ x\cdot \ln(10) - \ln(R_2)\right]\right\}\\ &\quad&\\ &=& 10\cdot\tanh\left[ x\cdot \ln(10) + \ln(R_2)\right] - 10 \cdot\tanh\left[ x\cdot \ln(10) - \ln(R_2)\right]\end{eqnarray}$
となります。
中心角周波数 $\omega = 1$ 、つまり $x = 0$ の点での勾配は、
$\qquad\qquad \begin{eqnarray}G^\prime(0) &=& 10\cdot\tanh\left(\ln(R_2)\right) - 10\cdot\tanh\left(-\ln(R_2)\right)\\&\quad&\\ &=& 20 \cdot\tanh\left(\ln(R_2)\right) \end{eqnarray}$
であり、これを -10 と等しいと置けば、
$\qquad\qquad G^\prime(0) = -10 = 20 \cdot\tanh\left(\ln(R_2)\right)$
$\qquad\qquad \tanh\left(\ln(R_2)\right) = - \frac{1}{\,2\,}$
$\qquad\qquad \ln(R_2) = -{\rm arctanh}\left(\frac{1}{\,2\,}\right)$
$\qquad\qquad R_2 = e^{-{\rm arctanh}(1/2)}$
となります。 arctanh の公式から、
$\qquad\qquad {\rm arctanh}\left(\frac{1}{\,2\,}\right) = \frac{1}{\,2\,} \ln\left(\frac{1 + 1/2}{1 - 1/2}\right) = \frac{1}{\,2\,} \ln(3)$
と表されるので、
$\qquad\qquad R_2 = e^{-\ln(3)/2} = \frac{1}{\sqrt{\,3\,}}= 0.57735...$
となります。　さらに、
$\qquad\qquad R_1 = \frac{1}{R_2}-R_2 = \sqrt{3} - \frac{1}{\sqrt{\,3\,}} =\frac{2}{\sqrt{\,3\,}} = 2 R_2 = 1.15470...$
となり、これが -3 dB/oct (-10 dB/dec) のスロープとなる条件です。