PIC18F14K50 (12)
以前から試してみたいと思っていた、ベース結合アンチログ回路の実験をしてみました。
それは、いわゆる「スーパー β (ベータ) トランジスタ」という、直流電流増幅率 (hFE) の非常に大きいトランジスタを使って、アンチログ回路のトランジスタを 1 個減らして 2 石で実現することです。
まず、基本の回路を下に示します。
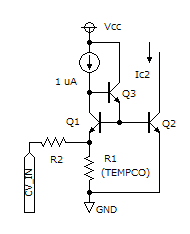
この回路は、「ベース電流補償型カレントミラー」を基にしており、トランジスタ Q2 のコレクタ電流がアンチログ回路の出力電流となります。
出力電流範囲を 1 μA 〜 1 mA の約 10 オクターブで動作させる場合には、カレントミラーの参照入力側のトランジスタ Q1 のコレクタ電流を、出力範囲の最低値の 1 μA に設定します。
CV 入力は R2 と R1 で分圧されて Q1 のエミッタに加えられます。
CV = 0 V の場合には、 VE1 = 0 V となって、本来のカレントミラーとして機能しますから、Q2 のコレクタ電流も 1 μA になります。
実際には Q1 のエミッタ電流 1 μA が R1 に流れるので、エミッタ電位は 0 V になりませんが、R1 = 1 kΩ とすると、その値は 1 μA * 1 kΩ = 1 mV の程度です。
また、R1 に温度補償抵抗を使えば、温度によるオクターブ・スパンのずれを補正できます。
CV 入力に電圧を加え、VE1 = 180 mV 程度になると Q1 と Q2 のコレクタ電流比は 1000 程度になり、出力電流 IC2 = 1 μA * 1000 = 1 mA の最大値になります。
Q2 の hFE を 100 程度とすると、コレクタ電流 1 mA に対してはベース電流を 10 μA 程度流す必要があります。
この Q2 のベース電流を供給しているのがトランジスタ Q3 です。
Q3 もバイポーラ・トランジスタですから、ベース電流を流す必要があり、同じく hFE を 100 程度とすると、Q3 のベース電流は、10 μA / 100 = 0.1 μA となります。
このベース電流 0.1 μA は Q1 のコレクタ電流を流している回路から「横取り」しているので、その分はピッチの「誤差」となります。
Q2, Q3 の hFE を 100 程度とすると、結局、Q3, Q2 が hFE = 100 * 100 = 10000 の「ダーリントン・トランジスタ」のように作用していることになります。
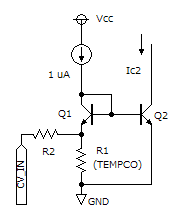
ここで、Q1, Q2 の hFE が非常に高ければ、(Q2の) ベース電流補償用の Q3 を省略して、左図のような Q1 をダイオード接続した基本型 (Widlar 型) のカレントミラーの構成を使うことができます。
スーパーベータトランジスタは、東芝の製品でいえば、
- 2SC3112 (TO-92 パッケージ)
- 2SC3113 (Mini パッケージ)
- 2SC3295 (SC-59 バッケージ、0.95 mm ピッチ)
- 2SC4666 (SC-70 バッケージ、0.65 mm ピッチ)
があります。
おそらく、半導体のダイは同一で、パッケージだけが違うラインナップであると思われます。
hFE の区分は、「A」が 600 〜 1200、「B」が 1200 〜 3600 です。
表面実装型は扱いにくいし、かと言って、いまさら TO-92 パッケージでもないだろうということで、4 mm x 3 mm 程度のサイズの Mini パッケージの 2SC3113 の B ランクを購入しました。 (サトー電気で単価 21 円)
テスタで hFE を測ってみると 1600 〜 1900 程度で、2000 を超えるものはありませんでした。
値としては十分高いのですが、通常の「ダーリントン」構成では 10000 以上となるので、通常の構成に比べれば、回路の簡単化の代償として、誤差の少ない範囲が狭くなります。
hFE が 1900 程度の 2SC3113 を 2 個使用した回路で、実際に測定した結果を下に示します。
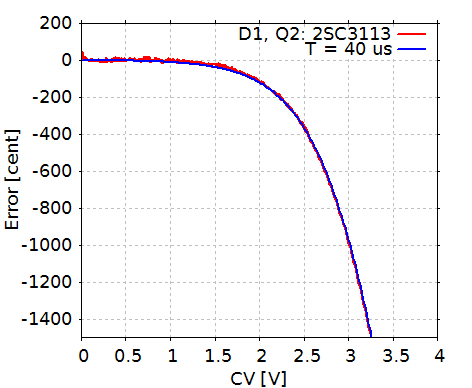
赤い線が実測値で、いつものように 4 回連続で測定したのですが、1 回目の測定は誤差が大きかったので 3 回分の結果のみプロットしてあります。
青い線がリセット時間に換算した誤差の出方を示すもので、リセット時間 40 μs 相当のカーブに測定結果が良く一致しています。
これは、低い電流値からベース電流による誤差が出始めているので、大電流領域でのトランジスタ固有の誤差要因があまり顕著に表れないことと、Q1 の設定電流の変化が少なくなっているためだと思います。
誤差が半音、つまり 100 セント程度に達するのが CV 入力では 2 V 程度のところであることが読み取れます。
R2 = 15 kΩ, R1 = 1 kΩ なので、差動電圧としては 120 mV 程度になり、オクターブに換算すると、約 6.5 オクターブのレンジとなります。
Franco の補償をかければレンジを広げられますが、誤差量のリセット時間換算が 40 μs と大きいので、周波数が 20 kHz の場合、周期は 50 μs しかなく、のこぎり波の補償後の振幅は 1/5 になってしまいます。
振幅が 1/2 になる条件では、周波数は 12.5 kHz となります。
高い周波数で、あまり振幅が小さくならないようにするには、
- Q1 の設定電流値を大きくする
- タイミング・コンデンサの容量を小さくする
ことにより、全体の周波数を高い方にシフトする必要があります。 これにより、下限の周波数も引き上げられ、低い周波数が出せなくなります。
次回以降では、この回路で Franco の補償をかけた場合の測定と、通常の 3 トランジスタ回路の一部/全部をスーパーベータトランジスタに置き換えた場合の測定をしてみたいと思います。