別のアンチログ回路 (2) -- アナログシンセの VCO ブロック (39)

アナログシンセ回路 VCO アンチログ SPICE

まず、文献 [*1] の中の

  • 第５章 増幅回路、5.6 差動電流増幅回路(4)、pp.127、
    図5.10 出力電流が指数的に増大する差動電流増幅回路

について説明します。

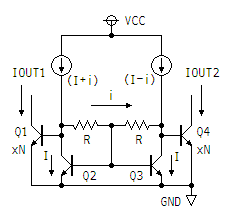
左の図が図5.10 に相当するもので、電圧入力ではなく、「差動電流」入力に対して「差動電流」出力を得るもので、その出力電流が指数関数となるものです。
出力電流を「差動」と書きましたが、正確には、ふたつの電流の「積」が一定で、「比」が変化します。
図で Vcc につながっている２つの電流原が差動電流入力で、一定のバイアス電流 I (ラージ・アイ) に、左の電流原では差動電流分の i (スモール・アイ) を足した値、右の電流原では i を引いた値が流れるものとします。
Q1、Q4 のエミッタの近くに「xN」と書いてあるのは、エミッタ面積が Q2、Q3 の N 倍になっていることを示しています。　ここでは簡単のため、エミッタ面積は全てのトランジスタで等しく、特性は揃っており、さらに、ベース電流は無視できるものとします。
Q2 と Q3 のトランジスタはお互いにベースとエミッタが接続されているので、 Vbe2 = Vbe3 となり、Ic2 = Ic3、つまり、互いのコレクタ電流も等しくなります。
いま、ベース電流は無視しているので、２つの電流源から流れ出した電流 (I+i) + (I-i) = 2*I はすべて Q2、Q3 のコレクタからエミッタを介してグラウンドに流れ込みます。
Ic2 = Ic3 なので、計 2*I の電流は Q2 側、Q3 側の両方に等しく I ずつ分かれて流れます。　これは、差動電流の値 i に依存しません。
左側の電流源は (I+i) を流そうとする一方で、Ic2 は I しか流れませんから、その差である i は Q2 のコレクタにつながっている抵抗 R に流れ込みます。
同様に、右側の電流源は (I-i) を流そうとする一方で、Ic3 は I だけ流そうとするので、その差の i だけ足りない電流を右側の抵抗 R から Q3 のコレクタへ引き込みます。
結局、図に示したように、差動電流 i は直列になっている２つの抵抗 R を介して流れることになります。
Q2 と Q3 のベース電圧は等しく、これを Vb とおくと、Vb = Vb2 = Vb3 です。　したがって、抵抗での電圧降下を考慮すると、

  • 左の R の左端の電圧 = Vb1 = Vc2 = Vb + i*R
  • 右の R の右端の電圧 = Vb4 = Vc3 = Vb - i*R

が成り立つことが分かります。
Q2、Q3 に流れているコレクタ電流はともに等しく I ですから、そのベース電圧 Vb とコレクタ電流の関係は、
\qquad\qquad I = I_{\mathrm\fs1 S} \cdot \exp(V_{\mathrm\fs1 B}/V_{\mathrm\fs1 T})
\qquad\qquad V_{\mathrm\fs1 B} = V_{\mathrm\fs1 T} \cdot ( \log(I) -\log(I_{\mathrm\fs1 S}) )
となります。
また、トランジスタ Q1 のベース電圧 Vb1 とコレクタ電流 Ic1 = 出力電流 Iout1 との関係は、
\qquad\qquad \begin{eqnarray} I_{\mathrm\fs1 OUT1} &=& I_{\mathrm\fs1 C1} = I_{\mathrm\fs1 S}\, \cdot\, \exp(V_{\mathrm\fs1 B1}/V_{\mathrm\fs1 T}) \\ \vspace{10pt} \\ &=& I_{\mathrm\fs1 S}\, \cdot\, \exp((V_{\mathrm\fs1 B} + i \cdot R)/V_{\mathrm\fs1 T}) \\ \vspace{10pt} \\ &=& I \cdot\, \exp(\, i \cdot R/V_{\mathrm\fs1 T}) \end{eqnarray}
となり、出力電流 Iout1 はバイアス電流 I に比例し、入力差動電流 i のエクスポネンシャルに比例することが分かります。
同様にして、Q4 側の Iout2 については
\qquad\qquad I_{\mathrm\fs1 OUT2} = I \cdot\,\exp( -i \cdot R/V_{\mathrm\fs1 T})
となります。
これらの式には、熱電圧 Vt は含まれていますが、逆方向飽和電流 Is の寄与は含まれておらず、通常の差動ペアによるアンチログ回路と同様の特性となっています。
抵抗 R に 1/T、つまり 300 K で約 3300 ppm/K の正の温度特性を持たせれば、温度によるオクターブ・スパンの変化を補償することができます。
この回路を見たときに、差動電流入力で差動電流出力の回路として、最初は気にとめなかったのですが、よく見れば、電流出力の片側だけ使ってアンチログ回路として応用できることに気付いたのです。
そういうわけで、Q4 側だけ使うことにして、不要な Q1 は全く省略し、Q2 につながっている抵抗 R は取り去って Q2 はダイオード接続にして使っています。
これまでの議論で無視していたトランジスタのベース電流の影響についてですが、Q2、Q3 については影響が少なく、あまり問題になりません。
ベース電流を無視した場合には、差動入力電流 i = 0 なら抵抗 R を流れる電流もゼロになりますが、実際には Q2、Q3 のベース電流 Ib は抵抗 R を介して供給されるので、i = 0 でもベース電流 Ib による電圧降下が生じることになります。
ベース電流 Ib = I / (hFE+1) となるので、値も小さく、また、差動入力電流 i に依存しない一定値となるので、Q1、Q4 のベース電圧には微少な一定値のオフセットが加わるだけの効果となります。
Q1、Q4 のベース電流による誤差は無視できず、考えた回路では OP-07 などの入力バイアス電流補償に使われている回路でベース電流補償を行いました。(Q9、Q10、Q11)　その動作については以前説明しているので省略します。

*1:青木 英彦 著:「アナログICの機能回路設計入門―回路シミュレータSPICEを使ったIC設計法 (C&E TUTORIAL)」、CQ出版 (1992年9月)、ISBN:4789832910