Gilbert Sine Shaper (9)
これまで求めてきた式の導出過程を振り返ると、g(x) を(もちろん実関数の)奇関数という仮定のみから変形してゆき、奇数次の高調波成分からなるフーリエ級数形式の結果を得ました。
GSS 回路の入力電圧 Va に対して、
- 2E を周期とする周期関数
- 偶数次高調波は存在しない
という性質は、隣合う差動ペアのとのオフセットは E であり、そのコレクタ出力は互いに逆極性に加算していくという「構造」そのものから導きだされており、g(x) の具体的な形には依存していません。
g(x) は、その(逆)フーリエ変換 G(y) を通じて、高調波成分の振幅を決定する形になっています。
三角関数である sin 関数を近似するのに、双曲線関数である tanh 関数を使っているのには特別な意味があるわけではなく、「奇関数のS字カーブ」の関数なら、この方式でのサイン関数発生に使えて、その関数の形により高調波成分の割合が変わるだけです。
「S字カーブ」と言われて、まっさきに浮かぶのが「ロジスティック曲線」ですが、これは本質的に tanh 関数なので、バイポーラ・トランジスタの差動ペアによる実現と同じです。
「ゴンペルツ曲線」はS字カーブですが対称性がないので使えません。
次に浮かぶのが、正規分布の累積分布関数(誤差関数)で、現実の回路素子としては存在しませんが、試してみたところ、大変良い結果が得られました。
現実の回路素子としては、単体では2乗特性になる FET を使った差動ペアがありますが、こちらでは、あまり思わしくない結果となりました。 プログラムのミスによるものかも知れないので、もう少しトライしてみます。
各種の「S字カーブ」とサイン波形をプロットしてみました。 x=0 の点での傾きが1になるように揃えてあります。
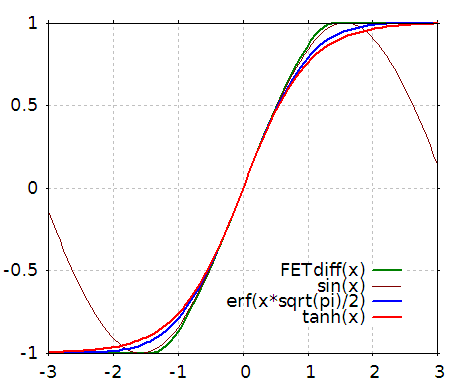
緑色の線が FET 差動ペア、茶色の線がサイン関数、青の線が誤差関数、赤の線が tanh 関数です。
グラフとしてはわずかの差ですが、結果の高調波のレベルには大きな差があります。
次回は誤差関数を使った場合について述べます。