シュトレーレ回路 (2) -- シュトレーレ・アッテネータ (1)

OP アンプと可変抵抗を使用した反転増幅回路で、回路定数の決定に「シュトレーレ近似」を使い、6 dB の範囲内でゲインを連続可変可能な回路を、ここでは「シュトレーレ・アッテネータ」と呼ぶことにします。
反転増幅回路ですから、「アッテネータ」といっても減衰一方ではなく、-3 dB から +3 dB までの範囲でゲインが変化します。
下の図のように、固定抵抗 R1、R2、可変抵抗 R3 を組み合わせて可変ゲイン反転増幅回路を構成します。

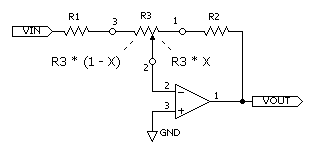
回転角と抵抗値がリニアに比例する、Ｂカーブの可変抵抗器のスライダ (2 番端子) の抵抗体上の相対位置を x で表すことにします。
x = 0 は、つまみを反時計回り一杯に回し切った状態で、スライダは 1 番端子と接触する位置にあるものとします。
同様に x = 1 は、つまみを時計回り一杯に回し切った状態で、スライダは 3 番端子と接触する位置にあるものとします。
x = 0.5 は、つまみは中間の状態で、1 - 2 間の抵抗値と 3 - 2 間の抵抗値が等しくなるものとします。
この x と、可変抵抗全体の抵抗値 R3 を使って 1 番端子と 2 番端子の間の抵抗値を表現すると、

となり、同様に 1 番端子と 3 番端子の間の抵抗値は

と表されます。
これから反転増幅回路のゲイン を求めると、

となります。
一方、シュトレーレの近似式を変形していくと、

と求められます。
係数 (10/7) は別にして、前出のゲインの式と比べると、


となります。
つまり、フィードバック側の固定抵抗 R2 は R3 の 2.4 倍、入力側の固定抵抗 R1 は R3 の約 2.43 倍に選べばシュトレーレの近似式を満足します。
可変抵抗 R3 を 10 kΩ とすると、次の図のように R1 = 24.3 kΩ、R2 = 24 kΩ です。

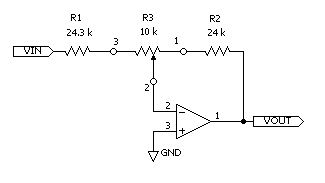
回路は簡単で、製作も容易ですが、可変抵抗の「x」つまり回転角を高精度に求めることが難しいので、実際に回路を作る前に SPICE シミュレーションで確かめてみました。
下は LTSpice の回路図入力です。 OP アンプ部は電圧制御電流源 (G) で代用してあります。

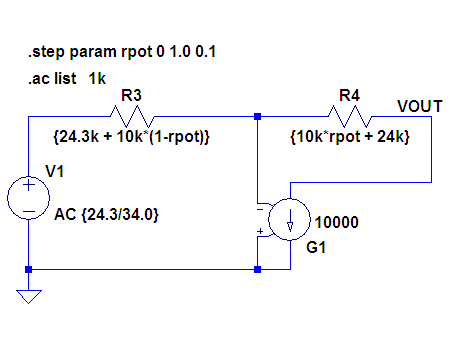
抵抗値がゼロになると怒られるので、R1, R2 の分も取り込んで可変抵抗を定義してあります。
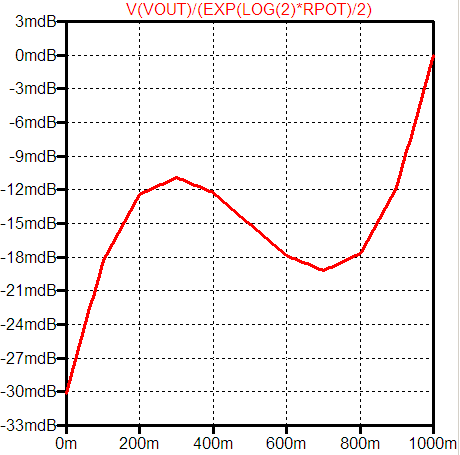
結果の誤差のグラフを次に示します。

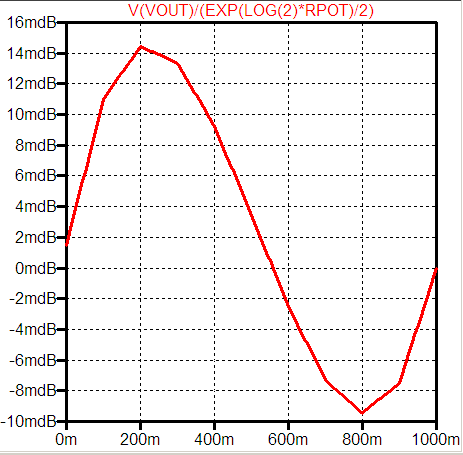
誤差が大きくなるのを覚悟で、R1 を 24 kΩ に変えた場合の結果を下に示します。