FPGA 版 FM 音源 (82) -- TX7 (OPS) 測定 (9)
2014 年 5 月 6 日の記事 (→こちら) の OPM の EG 測定と同様に、正弦波出力のオペレータ 2 段による直列 FM で、下のグラフのようなピーク部分が平坦な「方形波」を発生させ、EG の動作を探っています。
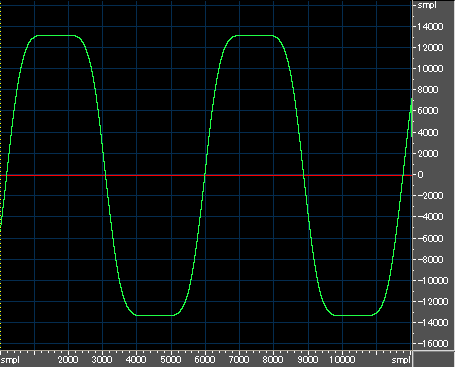
これは、「イニシャル・ボイス」のオペレータ 2 の出力レベルを「62」として発生させた方形波をキャプチャし、波形編集ソフトで表示したものです。
ADSR タイプの EG での「アタック・レート」に相当する「R1」を 40 に選び、「リリース・レート」に相当する「R4」を同じく 40 に選んだ場合の「エンベロープ」波形を下に示します。
オペレータ出力波形の周波数は 2 kHz 程度です。
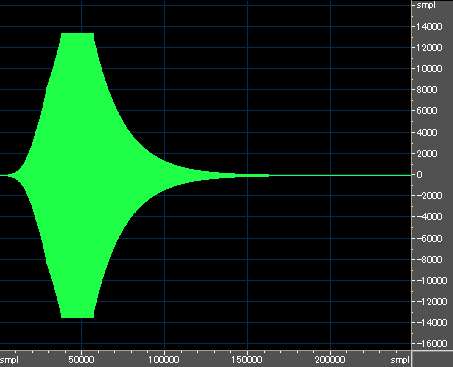
「アタック」部分はまだ良く調べていないので OPL や OPM, OPN のような「ゴンペルツ・カーブ」かどうかは分かりません。
「リリース」部分は、単純な単一のエクスポネンシャル・カーブなので、リリース部分を先に調べることにしました。
まず、波形編集ソフトの「時間反転機能」で、時間方向に逆向きの波形とします。
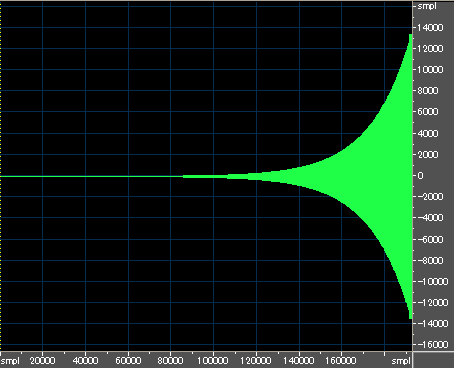
そうすると、ピーク部分の値は単調増加となるので、正負やゼロの値を取る出力波形の値そのものではなく、「波形の絶対値の最大値」を保持していけば、実質的に波形のピーク部分だけの寄与を得ることができます。
そうして得られたピーク値の 2 を底とする対数を計算して y 軸とし、サンプル・インデクスを x 軸としてプロットしたのが下の図です。
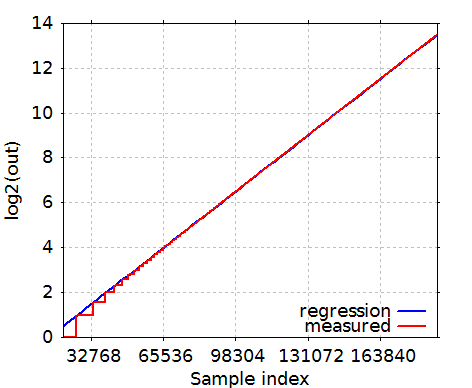
赤色のトレースが測定値であり、青色のトレースは
y(x) = a * x + b
で定義される直線に Gnuplot の機能でフィッティングさせた「回帰直線」です。
測定値のトレースが値の小さい部分で「荒い」階段状のステップになっているのは、DAC の量子化ステップの寄与が値の小さい部分では相対的に大きくなってくるためです。
DX7 / TX7 では EG レート・パラメタ値が「6」増加すると実際のレートは 2 倍になるので、R4 パラメタ値が 40 から 46 までの設定に対し、同様の測定を行ない、上述の回帰直線の係数 an を求めて表にしたものを下に示します。
| RATE | an | 1/an | an/a40 | (1<<16) * an |
|---|---|---|---|---|
| 40 | 7.638e-05 | 13092.1 | 1.0000 | 5.006 |
| 41 | 9.168e-05 | 10908.0 | 1.2002 | 6.008 |
| 42 | 9.166e-05 | 10909.8 | 1.2000 | 6.007 |
| 43 | 1.069e-04 | 9353.1 | 1.3998 | 7.007 |
| 44 | 1.226e-04 | 8158.8 | 1.6047 | 8.033 |
| 45 | 1.224e-04 | 8171.1 | 1.6023 | 8.020 |
| 46 | 1.528e-04 | 6542.8 | 2.0010 | 10.017 |
表の第 2 カラムは回帰直線の係数値 an であり、第 3 カラムはその逆数を表示しています。
2 を底とする対数を取っているので、第 3 カラムは「半減期」、つまりレベルが -6 dB 減衰するに要するサンプル数となります。
第 4 カラムは R4 = 40 の場合の係数 a40 との比率を表しており、
- R4 = 41 では 1.2 倍
- R4 = 42 では 1.2 倍
- R4 = 43 では 1.4 倍
- R4 = 44 では 1.6 倍
- R4 = 45 では 1.6 倍
- R4 = 46 では 2.0 倍
となっていることが分かります。
第 5 カラムは回帰直線の係数値 an を 16 ビット左シフトしたもの、つまり、65536 倍したもので、
- R4 = 40 では 5
- R4 = 41 では 6
- R4 = 42 では 6
- R4 = 43 では 7
- R4 = 44 では 8
- R4 = 45 では 8
- R4 = 46 では 10
となっていることが分かります。
これは、
- 「長い」EG アキュムレータに数値 5 / 6 / 7 / 8 をレートに応じてシフトした上で加算していくか、
- 「短い」EG アキュムレータ + 3 ビット・レート・マルチプライア + EG クロック・プリスケーラ
で実現できます。