SPI ハードウェア CRC 回路の MMC/SD カードへの応用 (3)

前回述べたように、実際の STM32 の SPI モジュールのハードウェア CRC 計算回路で求まるのは、8 ビットの「0」を追加した入力メッセージに対する剰余ですが、それについては後に回し、まず、定義通りの場合について考えます。
40 ビットの入力メッセージに 7 ビットの「0」を追加し、47 ビットとした入力メッセージ多項式を 8 次の生成多項式で割った余りの多項式を「r_{8_47}(x)」として、下の式で定義します。
r_{8_47}(x) = (x⁷・M(x)) mod (x⁸ + x⁷ + x⁴ + x³ + x + 1)
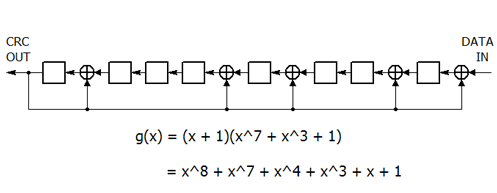
これは、47 ビットの入力メッセージを下図の原理的な回路で計算したものに相当します。

「r_{8_47}(x)」から、求める CRC-7 の値「r_{7_47}(x)」を求めるのは簡単で、単に「r_{8_47}(x)」を CRC-7 の生成多項式 (x⁷ + x³ + 1) で割って余りの多項式を求めれば良いのです。
式で表現すれば、
    r_{8_47}(x) = q(x)・(x⁷ + x³ + 1) + r_{7_47}(x)
となります。
ここで、商 q(x) の値は「0」か「1」です。
r_{8_47}(x) は 8 次の多項式で割った余りなので、その次数は 7 以下となります。　したがって、7 次の多項式 (x⁷ + x³ + 1) で割れるかどうかは、r_{8_47}(x) の 7 次の項の係数を見れば判定できます。
7 次の項の係数が「1」なら割れて、「0」なら割れません。
係数が「0」で、割れない場合には商 q(x) はゼロですから、
    r_{8_47}(x) = r_{7_47}(x)
となり、8 次の多項式で割った余り r_{8_47}(x) そのものが目的の CRC-7 の値となっています。
7 次の項の係数が「1」で、割れる場合には商 q(x) は 1 ですから、
    r_{7_47}(x) = r_{8_47}(x) - (x⁷ + x³ + 1)
となります。
ここで、この演算は GF(2)、つまり、元が「0」と「1」しかない有限体上に係数を持つ多項式の演算ですから、「加算」と「減算」は同じ演算となり、具体的には「エクスクルーシブ OR」で実現されます。
以上の「補正」手続きを C 言語風に表現すると、8 次の多項式でメッセージ多項式を割った余りを保持している変数を「crc_value」として、

// CRC-7: g(x) = x**7 + x**3 + 1
//             = {7, 3, 0}
//             = 0x89
//             = 0b10001001

  #define GX_CRC7 (0x89)

  if (0x80 & crc_value) { 
    crc_value ^= GX_CRC7;
  }

のようになります。
このプログラムと、10 月 9 日付けの記事のプログラムとでは、「1」かどうかを検査するビット位置が b7 か b0 かという違いがあります。
それは、入力メッセージに追加する「0」の数が 7 個か 8 個かの違いに起因するのですが、その話は次回に回します。