SPI ハードウェア CRC 回路の MMC/SD カードへの応用 (2)

CRC-7 の生成多項式に単一パリティの因子 (x + 1) を掛けて求めた 8 次の多項式を使って計算した結果から、もとの CRC-7 に対応する結果を抽出する方法を説明していきます。
まず、CRC-7 をビット・シリアルに計算する回路を下に示します。

MMC/SD カードの SPI モードでは、データおよびコマンドは、CRC の部分も含めて MSB ファーストで送られるので、それに合わせ、シフトレジスタは左にシフトする表現にしています。
CRC を計算する対象となるのは、コマンド 8 ビット (固定パターン 2 ビット、インデクス 6 ビット) およびその引数 32 ビットの合計 40 ビットです。
この 40 ビットの「メッセージ」に対して、次のような手順で CRC を生成します。

シフトレジスタの全ビットを「0」にクリア
メッセージ 40 ビットを入力
7 ビット分の「0」を入力

3 番の「7 ビット分のゼロ」というのは、最後尾の固定ビット 1 ビットを除いた 47 ビットの出力シーケンスの中で、CRC の値が格納される部分に相当します。
送信側の CRC 生成では、出力シーケンスの CRC の部分をゼロにした 47 ビット・シーケンスに対して上の回路で CRC の計算を行い、得られた 7 ビットの結果を 47 ビット・シーケンスに埋め込んで送出します。
受信側では、受信した 47 ビット・シーケンスをそのまま連続して CRC 計算を行い、結果のシフトレジスタの内容がオールゼロになれば、エラーがなかったことが確認できます。
メッセージの 40 ビットをひとつのワードと考え、先頭のビットを b₃₉、最後尾のビットを b₀ と書いて、「メッセージ多項式」として表現すると、
    M(x) = b₃₉・x³⁹ + b₃₈・x³⁸ + ... + b₁・x + b₀
のようになります。
この多項式表現で、7 ビットの「0」を追加するのは、x の 7 乗を掛ければよく、
    x⁷・M(x) = b₃₉・x⁴⁶ + b_38・ x⁴⁵ + ... + b₁・x⁸ + b₀・x⁷
となります。
MMC/SD カードでの CRC 計算を多項式表現で式として表すと、
    r₇(x) = (x⁷・M(x)) mod (x⁷ +　x³ + 1)
メッセージ多項式 M(x) に x⁷ を掛けたものを、CRC-7 の生成多項式 g₇(x) = (x⁷ + x³ + 1) で割った余り r₇(x) が求める CRC の値ということです。
上の回路は、定義に忠実な構成となっていますが、CRC を求めるのに途中で余分な「0」を入力する必要があり、それを嫌って、実際には下の図のような、別の回路が良く使われます。

この回路では、メッセージ多項式 40 ビット分を入力した段階で、シフトレジスタ内に目的の CRC の値が得られます。　余分な 7 ビットの「0」を入力する必要はありません。
なぜ、この回路で余分なゼロが必要ないのかを定性的に簡単に説明します。
まず、元の回路では、最初にシフトレジスタの内容がクリアされているので、最初の 7 ビット分は常に「0」がシフトアウトされてきて、フィードバックされるビットも「0」となり、シフトインされる入力データに影響を与えません。
つまり、最初の 7 ビット分は、入力データが単にシフトレジスタにシフトインされていくだけで、LFSR の特徴である「フィードバック」は機能していません。
したがって、データビットの入力が終わっても、追加で 7 ビット分シフトしなければ結果が得られないことになります。
それに対して、この回路では、入力データはフィードバック・パスに直接作用しているので、入力データの最初の 1 ビット目からフィードバックが変化します。
したがって、余分なシフトは必要ありません。
STM32 の SPI モジュールの CRC 計算回路も、この回路に類した構成となっていると思われます。
CRC-7 の生成多項式に (x + 1) を掛けた生成多項式に対する回路を下に示します。

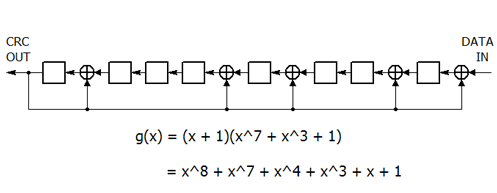
これは、定義に忠実な構成の回路です。
フィードバック・パスに入力するタイプの回路を下に示します。

ここで注意するべきことは、シフトレジスタが 8 ビット幅なので、この回路で計算される CRC の値は、原理に忠実な回路で入力メッセージのあとに追加の 8 ビットの「0」を入力したものに相当しています。
当然、STM32 の SPI モジュールの CRC 計算回路で計算した値も同様となります。
正しくは、追加の「0」は 7 ビットですから、1 ビット分余計に「0」が入力されることに対する補正も必要になってきます。　それについては後で述べます。
以下、次回に続きます。